10. Summary of Propositional Logic
10.1 Elements of the language
Principle of Bivalence: each sentence is either true or false, never both, never neither.
Each atomic sentence is a sentence.
Syntax: if Φ and Ψ are sentences, then the following are also sentences
-
- ~Φ
- (Φ→Ψ)
- (Φ&Ψ)
- (ΦvΨ)
- (Φ↔Ψ)
Semantics: if Φ and Ψ are sentences, then the meanings of the connectives are fully given by their truth tables. These truth tables are:
| Φ | ~Φ |
|---|---|
| T | F |
| F | T |
| Φ | Ψ | (Φ→Ψ) |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
| Φ | Ψ | (Φ&Ψ) |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
| Φ | Ψ | (Φ v Ψ) |
|---|---|---|
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
| Φ | Ψ | (Φ↔Ψ) |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
A sentence of the propositional logic that must be true is a tautology.
A sentence that must be false is a contradictory sentence.
A sentence that is neither a tautology nor a contradictory sentence is a contingent sentence.
Two sentences Φ and Ψ are equivalent, or logically equivalent, when (Φ↔Ψ) is a theorem.
Translation key: English to propositional logic
| Translation key: English to propositional logic | |
| Logic | English |
| P | P
Not not P |
| ~~P | P
Not not P |
| (P→Q) | if P, then Q
since P, Q Q, if P On the condition that P, Q Q, on the condition that P given that P, Q Q, given that P provided that P, Q Q, provided that P when P, then Q Q, when P P implies Q Q is implied by P P is sufficient for Q Q is necessary for P P only if Q Only if Q, P …and so on |
| ~(P→Q) | it is false that if P then Q |
| ~P | it is not the case that P
Not P un-P …and so on |
| (P & Q) | P and Q
even though P, Q. although P, Q in addition to Q, P P but Q P however Q P moreover Q P nevertheless Q P nonetheless Q …and so on |
| (PvQ) | P or Q
Either P or Q P and/or Q …and so on |
| ((PvQ) & ~ (P & Q)) | P or Q but not both
P xor Q …and so on |
| ~(P&Q)
(~Pv~Q) |
not both P and Q
…and so on |
| ~(PvQ)
(~P & ~ Q) |
neither P nor Q
…and so on |
| (~P→ Q)
(~Q→P) (PvQ) |
P unless Q
…and so on |
| (P↔Q) | P if and only if Q
P just in case Q whenever P, Q and whenever Q, P P is necessary and sufficient for Q. P is equivalent to Q. …and so on |
Notes:
- Atomic sentences are always in the affirmative.
- If the meaning of a complex English sentence cannot be captured by a dependent sentence, translate it as an atomic sentence.
- Negations attach to only one sentence (that sentence may be atomic or dependent).
- Conditionals, conjunctions, disjunctions, and biconditionals each connect two and only two sentences (those sentences may be atomic or dependent).
- There are only two kinds of syntactically acceptable sentences in propositional logic. 1) Atomic sentences, such as P; Q; R; S, and so on, represented by capital letters, or 2) dependent sentences such as (P→Q); ~P; (P & Q); (PvQ); (P↔Q), and combinations thereof, such as ((PvQ) & ~ (P & Q)).
10.2 Reasoning with the language
An argument is an ordered list of sentences, one sentence of which we call the “conclusion” and the others of which we call the “premises”.
A valid argument is an argument in which: necessarily, if the premises are true, then the conclusion is true.
A sound argument is a valid argument with true premises.
Inference rules allow us to write down a sentence that must be true, assuming that certain other sentences are true. We say that the new sentence is “derived from” those other sentences using the inference rule.
Schematically, we can write out the inference rules in the following way (think of these as saying, if you have written the sentence(s) above the line, then you can write the sentence below the line):
Rules of Inference
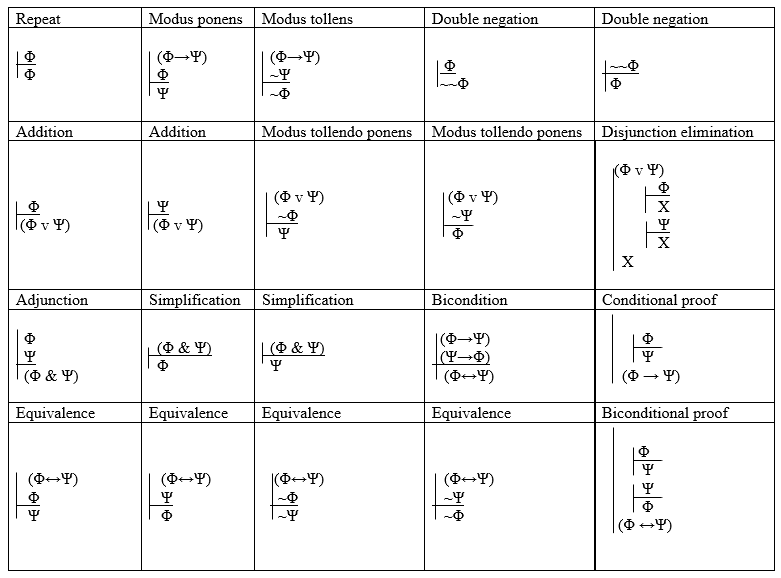
A proof (or derivation) is a syntactic method for showing an argument is valid. Our system has three kinds of proof (or derivation): direct, conditional, and indirect.
A direct proof (or direct derivation) is an ordered list of sentences in which every sentence is either a premise or is derived from earlier lines using an inference rule. The last line of the proof is the conclusion.
A conditional proof (or conditional derivation) is an ordered list of sentences in which every sentence is either a premise, is the special assumption for conditional derivation, or is derived from earlier lines using an inference rule. If the assumption for conditional derivation is Φ, and we derive as some step in the proof Ψ, then we can write after this (Φ→Ψ) as our conclusion.
An indirect proof (or indirect derivation, and also known as a reductio ad absurdum) is: an ordered list of sentences in which every sentence is either 1) a premise, 2) the special assumption for indirect derivation (also sometimes called the “assumption for reductio”), or 3) derived from earlier lines using an inference rule. If our assumption for indirect derivation is ~Φ, and we derive as some step in the proof Ψ and also as some step of our proof ~Ψ, then we conclude that Φ.
We can write out the three proof schemas in the following way:
![]()
![Rendered by QuickLaTeX.com \[ \fitchctx{ \subproof{\pline{\phi}}{ \ellipsesline\\ \pline{\psi} } \fpline{(\phi \lif \psi)} } \]](http://intrologicimport.pressbooks.tru.ca/wp-content/uploads/sites/9/2019/03/quicklatex.com-2f46df4a9e0479a7e59b3600a973707f_l3.png)
![Rendered by QuickLaTeX.com \[ \fitchctx{ \subproof{\pline{\lnot \phi}}{ \ellipsesline\\ \pline{\psi}\\ \pline{\lnot \psi} } \fpline{\phi} } \]](http://intrologicimport.pressbooks.tru.ca/wp-content/uploads/sites/9/2019/03/ex3.png)
A sentence that we can prove without premises is a theorem.
Suppose Φ is a theorem, and it contains the atomic sentences P1…Pn. If we replace each and every occurrence of one of those atomic sentences Pi in Φ with another sentence Ψ, the resulting sentence is also a theorem. This can be repeated for any atomic sentences in the theorem.
Replacement rules are pairs of logically equivalent sentences which may replace one another within proofs. They are special instances of the principle of replacement.
Rules of Replacement
| DeMorgans | Distribution |
| ~(Φ&Ψ) ↔ (~Φ v~Ψ)
~(ΦvΨ) ↔ (~Φ &~Ψ) |
(Φ&(Ψvμ)) ↔ ((Φ&Ψ)v(Φ&μ))
(Φv(Ψ&μ)) ↔ ((ΦvΨ) & (Φvμ)) |
| Commutation | Association |
| (Φ&Ψ) ↔ (Ψ&Φ)
(ΦvΨ) ↔ (ΨvΦ) |
((Φ&Ψ)&μ)↔ (Φ&(Ψ&μ))
((ΦvΨ)vμ)↔ (Φv(Ψvμ)) |
| Absorption | Transposition (T10) |
| Φ v (Φ&Ψ) ↔ Φ
Φ & (ΦvΨ) ↔ Φ |
(Φ →Ψ) ↔ (~Ψ → ~Φ)) |
| Tautology | Exportation |
| Φ↔(ΦvΦ)
Φ↔(Φ&Φ) |
((Φ& Ψ)→μ)↔((Φ →(Ψ→μ)) |
| Material implication | Material equivalence |
| (Φ→Ψ)↔ (~ΦvΨ) | (Φ↔ Ψ) ↔((Φ →Ψ) & (Ψ → Φ))
(Φ↔ Ψ) ↔((Φ →Ψ) & (Ψ → Φ)) |
Common and useful theorems
| T1 | T2 |
| (Φv~Φ) | (~Φ → (Φ → Ψ)) |
| T3 | T4 |
| (Φ → (Ψ → P)) | ((Φ →( Ψ →X)) → ((Φ → Ψ) → (Φ →X))) |
| T5 | T6 |
| ((~Φ →~ Ψ) → ((~Φ → Ψ) → Φ)) | (~(Φ ↔ Ψ) ↔ (Φ ↔ ~ Ψ)) |

