9.10 Exercises

A. Exercises: The Biconditional. Fill out the truth table for the following biconditionals.

1. P	Q	(P	↔	Q)
   T	T	T	T	T
   T	F	T	F	F
   F	T	F	F	T
   F	F	F	T	F

2. P	Q	(Q	↔	P)
   T	T	T	T	T
   T	F	F	F	T
   F	T	T	F	F
   F	F	F	T	F

B. Exercises: tautologies, contradictions and contingent sentences. True or False? Each of the following is possible.

1. A valid argument, the conclusion of which is a contradiction
   True. It is possible. Feedback: when the premises are inconsistent, they cannot be true; so there is no situation where the premises are true and the conclusion is false. The argument can be valid. E.g. Premise: Today is Monday. Conclusion: Therefore, it is raining and it is not raining.
2. An invalid argument, the conclusion of which is a tautology
   False. It is impossible. Feedback: when the conclusion is a tautology, the conclusion cannot be false; so there is no situation where the premises are true and the conclusion is false. The argument must be valid. E.g. Premise: Today is Monday. Conclusion: Therefore, it is raining or it is not raining.
3. A valid argument, the conclusion of which is a tautology
   True. It is possible. Feedback: when the conclusion is a tautology, the conclusion cannot be false; so there is no situation where the premises are true and the conclusion is false. The argument must be valid. E.g. Premise: Today is Monday. Conclusion: Therefore, it is raining or it is not raining.
4. An invalid argument, the conclusion of which is a contradiction
   True. It is possible. Feedback: so long as the premises are not inconsistent, they can be true while the conclusion is false. The argument can be invalid. E.g. Premise: Today is Monday. Conclusion: Therefore, it is raining and it is not raining.
5. A tautology that is contingent
   False. This is not possible.
6. Two logically equivalent sentences, both of which are tautologies
   True. Indeed, all tautologies are logically equivalent.
7. Two logically equivalent sentences, one of which is a tautology and one of which is contingent
   False. This is not possible.
8. Two logically equivalent sentences that together are an inconsistent set
   False. This is not possible.
9. A consistent set of sentences that contains a contradiction
   False. This is not possible.
10. An inconsistent set of sentences that contains a tautology
    True. This is possible.

C. Exercises: tautologies, contradictions and contingent sentences. Identify the following claims as tautology, contradiction, or contingent sentence.

1. If Caesar crossed the Rubicon, then someone has.
   It is a tautology: a claim that is true by logic alone.
2. Even though Caesar crossed the Rubicon, no one has ever crossed the Rubicon.
   It is a contradiction: a claim that is false by logic alone.
3. If anyone has ever crossed the Rubicon, it was Caesar.
   Feedback: This is a contingent sentence: We turn to common-sense to evaluate the claim.

D. Exercises: Truth tables, tautologies, contradictions and contingent sentences. Determine whether each sentence is a tautology, a contradiction, or a contingent sentence. Justify your answer with a complete truth table.

1. (P→P)
   

   P	(P	→	P)
   T	T	T	T
   F	F	T	F

   Look at the main logical connective, conditional. It is always true, so the sentence is a tautology.

2. (~Q&Q)
   

   Q	(~	Q	&	Q)
   T	F	T	F	T
   F	T	F	F	F

   Look at the main logical connective, conjunction. It is always false, so the sentence is a contradiction.

3. (R→~R)
   

   R	(R	→	~	R)
   T	T	F	F	T
   F	F	T	T	F

   Look at the main logical connective, conditional. It is true at least once and false at least once, so the sentence is contingent.

4. (Dv~D)
   

   D	(D	v	~	D)
   T	T	T	F	T
   F	F	T	T	F

   Look at the main logical connective, disjunction. It is always true, so the sentence is a tautology.

5. ((P↔Q)↔~(P↔~Q))
   

   P	Q	((P	↔	Q)	↔	~	(P	↔	~	Q))
   T	T	T	T	T	T	T	T	F	F	T
   T	F	T	F	F	T	F	T	T	T	F
   F	T	F	F	T	T	F	F	T	F	T
   F	F	F	T	F	T	T	F	F	T	F

   Look at the main logical connective, biconditional. It is always true, so the sentence is a tautology.

6. ((P&Q)∨(Q&P))
   

   P	Q	((P	&	Q)	v	(Q	&	P))
   T	T	T	T	T	T	T	T	T
   T	F	T	F	F	F	F	F	T
   F	T	F	F	T	F	T	F	F
   F	F	F	F	F	F	F	F	F

   Look at the main logical connective, disjunction. It is true at least once and false at least once, so the sentence is contingent.

7. ((P→Q)∨(Q→P))
   

   P	Q	((P	→	Q)	v	(Q	→	P))
   T	T	T	T	T	T	T	T	T
   T	F	T	F	F	T	F	T	T
   F	T	F	T	T	T	T	F	F
   F	F	F	T	F	T	F	T	F

   Look at the main logical connective, disjunction. It is always true, so the sentence is a tautology.

8. ~(P→(Q→P))
   

   P	Q	~	(P	→	(Q	→	P))
   T	T	F	T	T	T	T	T
   T	F	F	T	T	F	T	T
   F	T	F	F	T	T	F	F
   F	F	F	F	T	F	T	F

   Look at the main logical connective, negation. It is always false, so the sentence is a contradiction.

9. ((P&Q)→(Q∨P))
   

   P	Q	((P	&	Q)	→	(Q	v	P))
   T	T	T	T	T	T	T	T	T
   T	F	T	F	F	T	F	T	T
   F	T	F	F	T	T	T	T	F
   F	F	F	F	F	T	F	F	F

   Look at the main logical connective, conditional. It is always true, so the sentence is a tautology.

10. (P↔(P→(Q&~Q)))
    

    P	Q	((P	↔	(P	→	(Q	&	~	Q)))
    T	T	T	F	T	F	T	F	F	T
    T	F	T	F	T	F	F	F	T	F
    F	T	F	F	F	T	T	F	F	T
    F	F	F	F	F	T	F	F	T	F

    Look at the main logical connective, biconditional. It is always false, so the sentence is a contradiction.

11. (~(P∨Q) ↔ (~P&~Q))
    

    P	Q	(~	(P	v	Q)	↔	(~	P	&	~	Q))
    T	T	F	T	T	T	T	F	T	F	F	I
    T	F	F	T	T	F	T	F	T	F	T	F
    F	T	F	F	T	T	T	T	F	F	F	T
    F	F	T	F	F	F	T	T	F	T	T	F

    Look at the main logical connective, biconditional. It is true at least once and false at least once, so the sentence is contingent.

12. (~(P&Q)↔P)
    

    P	Q	(~	(P	&	Q)	↔	P)
    T	T	F	T	T	T	F	T
    T	F	T	T	F	F	T	T
    F	T	T	F	F	T	F	F
    F	F	T	F	F	F	F	F

    Look at the main logical connective, biconditional. It is true at least once and false at least once, so the sentence is contingent.

13. (((P&Q)&~(P&Q))&R)
    

    P

    Q

    R

    (((P

    &

    Q)

    &

    ~

    (P

    &

    Q))

    &

    R)

    T

    T

    T

    T

    T

    T

    F

    F

    T

    T

    T

    F

    T

    T

    T

    F

    T

    T

    T

    F

    F

    T

    T

    T

    F

    F

    T

    F

    T

    T

    F

    F

    F

    T

    T

    F

    F

    F

    T

    T

    F

    F

    T

    F

    F

    F

    T

    T

    F

    F

    F

    F

    F

    T

    T

    F

    F

    T

    F

    T

    F

    F

    T

    F

    T

    F

    T

    F

    F

    F

    T

    F

    T

    F

    F

    T

    F

    F

    F

    F

    T

    F

    F

    F

    F

    T

    F

    F

    F

    F

    T

    F

    F

    F

    F

    F

    F

    F

    T

    F

    F

    F

    F

    F

    Look at the main logical connective, conjunction. It is always false, so the sentence is a contradiction.

14. (P→(Q∨R))
    

    P	Q	R	(P	→	(Q	v	R))
    T	T	T	T	T	T	T	T
    T	T	F	T	T	T	T	F
    T	F	T	T	T	F	T	T
    T	F	F	T	F	F	F	F
    F	T	T	F	T	T	T	T
    F	T	F	F	T	T	T	F
    F	F	T	F	T	F	T	T
    F	F	F	F	T	F	F	F

    Look at the main logical connective, conditional. It is true at least once and false at least once, so the sentence is contingent.

15. (((P&Q) & R)→Q)
    

    P	Q	R	(((P	&	Q)	&	R)	→	Q)
    T	T	T	T	T	T	T	T	T	T
    T	T	F	T	T	T	F	F	T	T
    T	F	T	T	F	F	F	T	T	F
    T	F	F	T	F	F	F	F	T	F
    F	T	T	F	F	T	F	T	T	T
    F	T	F	F	F	T	F	F	T	T
    F	F	T	F	F	F	F	T	T	F
    F	F	F	F	F	F	F	F	T	F

    Look at the main logical connective, conditional. It is always true, so the sentence is a tautology.

16. ((P & ~P)→(Q∨R))
    

    P	Q	R	((P	&	~	P)	→	(Q	v	R)
    T	T	T	T	F	F	T	T	T	T	T
    T	T	F	T	F	F	T	T	T	T	F
    T	F	T	T	F	F	T	T	F	T	T
    T	F	F	T	F	F	T	T	F	F	F
    F	T	T	F	F	T	F	T	T	T	T
    F	T	F	F	F	T	F	T	T	T	F
    F	F	T	F	F	T	F	T	F	T	T
    F	F	F	F	F	T	F	T	F	F	F

    Look at the main logical connective, conditional. It is always true, so the sentence is a tautology.

17. ~((R∨P)∨Q)
    

    P	Q	R	~	((R	v	P)	v	Q)
    T	T	T	F	T	T	T	T	T
    T	T	F	F	F	T	T	T	T
    T	F	T	F	T	T	T	T	F
    T	F	F	F	F	T	T	T	F
    F	T	T	F	T	T	F	T	T
    F	T	F	F	F	F	F	T	T
    F	F	T	F	T	T	F	T	F
    F	F	F	T	F	F	F	F	F

    Look at the main logical connective, negation. It is true at least once and false at least once, so the sentence is contingent.

18. ((Q & R)↔(P↔(P∨R)))
    

    P	Q	R	((Q	&	R)	↔	(P	↔	(P	v	R)))
    T	T	T	T	T	T	T	T	T	T	T	T
    T	T	F	T	F	F	F	T	T	T	T	F
    T	F	T	F	F	T	F	T	T	T	T	T
    T	F	F	F	F	F	F	T	T	T	T	F
    F	T	T	T	T	T	F	F	F	F	T	T
    F	T	F	T	F	F	F	F	T	F	F	F
    F	F	T	F	F	T	T	F	F	F	T	T
    F	F	F	F	F	F	F	F	T	F	F	F

    Look at the main logical connective, biconditional. It is true at least once and false at least once, so the sentence is contingent.

E. Exercises: Consistency and inconsistency. Determine whether each set of sentences is consistent or inconsistent. Justify your answer with a complete truth table.

1. (P→P), (~P→~P), (P&P), (P∨P)
   

   P

   (P

   →

   P)

   (~

   P

   →

   ~

   P)

   (P

   &

   P)

   (P

   v

   P)

   T

   T

   T

   T

   F

   T

   T

   F

   T

   T

   T

   T

   T

   T

   T

   F

   F

   T

   F

   T

   F

   T

   T

   F

   F

   F

   F

   F

   F

   F

   Look at the columns for the main connectives; conditional for the first and second sentences, conjunction for the third and disjunction for the fourth. On the first row, all are true. Since there is at least one line of a complete truth table on which all of the sentences are true, the sentences are logically consistent.

2. (P&Q), (R→~Q), R
   

   P	Q	R	(P	&	Q)	(R	→	~	Q)
   T	T	T	T	T	T	T	F	F	T
   T	T	F	T	T	T	F	T	F	T
   T	F	T	T	F	F	T	T	T	F
   T	F	F	T	F	F	F	T	T	F
   F	T	T	F	F	T	T	F	F	T
   F	T	F	F	F	T	F	T	F	T
   F	F	T	F	F	F	T	T	T	F
   F	F	F	F	F	F	F	T	T	F

   Look at the columns for the main connectives; conjunction for the first, conditional for the second, and R itself for the third. There is no row where all are true. Since there is no row of a complete truth table on which all of the sentences are true, the sentences are logically inconsistent.

3. (P∨Q), (P→R), (Q→R)
   

   P	Q	R	(P	v	Q)	(P	→	R)	(Q	→	R)
   T	T	T	T	T	T	T	T	T	T	T	T
   T	T	F	T	T	T	T	F	F	T	F	F
   T	F	T	T	T	F	T	T	T	F	T	T
   T	F	F	T	T	F	T	F	F	F	T	F
   F	T	T	F	T	T	F	T	T	T	T	T
   F	T	F	F	T	T	F	T	F	T	F	F
   F	F	T	F	F	F	F	T	T	F	T	T
   F	F	F	F	F	F	F	T	F	F	T	F

   Look at the columns for the main connectives; disjunction for the first, conditional for the second, and third. On the first row, all are true. Since there is at least one row of a complete truth table on which all of the sentences are true, the sentences are logically consistent.

4. (P→Q), (Q→R), P, ~R
   

   P	Q	R	(P	→	Q)	(Q	→	R)	P	~	R
   T	T	T	T	T	T	T	T	T	T	F	T
   T	T	F	T	T	T	T	F	F	T	T	F
   T	F	T	T	F	F	F	T	T	T	F	T
   T	F	F	T	F	F	F	T	F	T	T	F
   F	T	T	F	T	T	T	T	T	F	F	T
   F	T	F	F	T	T	T	F	F	F	T	F
   F	F	T	F	T	F	F	T	T	F	F	T
   F	F	F	F	T	F	F	T	F	F	T	F

   Look at the columns for the main connectives; conditional for the fist two, P for the third, and negation for the fourth. There is no row where all are true. Since there is no row of a complete truth table on which all of the sentences are true, the sentences are logically inconsistent.

5. (Q&(R∨P)), (P→Q), ~(Q∨R)
   

   P

   Q

   R

   (Q

   &

   (R

   v

   P))

   (P

   →

   Q)

   ~

   (Q

   v

   R)

   T

   T

   T

   T

   T

   T

   T

   T

   T

   T

   T

   F

   T

   T

   T

   T

   T

   F

   T

   T

   F

   T

   T

   T

   T

   T

   F

   T

   T

   F

   T

   F

   T

   F

   F

   T

   T

   T

   T

   F

   F

   F

   F

   T

   T

   T

   F

   F

   F

   F

   F

   T

   T

   T

   F

   F

   T

   F

   F

   F

   F

   T

   T

   T

   T

   T

   T

   F

   F

   T

   T

   F

   T

   T

   T

   F

   T

   F

   T

   F

   F

   F

   F

   F

   T

   T

   F

   T

   T

   F

   F

   F

   T

   F

   F

   T

   T

   F

   F

   T

   F

   F

   F

   T

   T

   F

   F

   F

   F

   F

   F

   F

   F

   F

   T

   F

   T

   F

   F

   F

   Look at the columns for the main connectives; conjunction for the first, conditional for the second, and negation for the third. There is no row where all are true. Since there is no row of a complete truth table on which all of the sentences are true, the sentences are logically inconsistent.

6. (P∨Q), (Q∨R), (R→~P)
   

   P

   Q

   R

   (P

   v

   Q)

   (Q

   v

   R)

   (R

   →

   ~

   P)

   T

   T

   T

   T

   T

   T

   T

   T

   T

   T

   F

   F

   T

   T

   T

   F

   T

   T

   T

   T

   T

   F

   F

   T

   F

   T

   T

   F

   T

   T

   T

   F

   F

   T

   T

   T

   F

   F

   T

   T

   F

   F

   T

   T

   F

   F

   F

   F

   F

   T

   F

   T

   F

   T

   T

   F

   T

   T

   T

   T

   T

   T

   T

   T

   F

   F

   T

   F

   F

   T

   T

   T

   T

   F

   F

   T

   T

   F

   F

   F

   T

   F

   F

   F

   F

   T

   T

   T

   T

   T

   F

   F

   F

   F

   F

   F

   F

   F

   F

   F

   F

   T

   T

   F

   Look at the columns for the main connectives; disjunction for the first two, conditional for the third. On the second, fifth and sixth row, all are true. Since there is at least one row of a complete truth table on which all of the sentences are true, the sentences are logically consistent.

7. (P↔(Q∨R)), (R→~P), (P→~Q)
   

   P

   Q

   R

   (P

   ↔

   (Q

   v

   R))

   (R

   →

   ~

   P)

   (P

   →

   ~

   Q)

   T

   T

   T

   T

   T

   T

   T

   T

   T

   F

   F

   T

   T

   F

   F

   T

   T

   T

   F

   T

   T

   T

   T

   F

   F

   T

   F

   T

   T

   F

   F

   T

   T

   F

   T

   T

   T

   F

   T

   T

   T

   F

   F

   T

   T

   T

   T

   F

   T

   F

   F

   T

   F

   F

   F

   F

   F

   T

   F

   T

   T

   T

   T

   F

   F

   T

   T

   F

   T

   T

   T

   T

   T

   T

   T

   F

   F

   T

   F

   T

   F

   T

   F

   F

   T

   T

   T

   F

   F

   T

   T

   F

   F

   T

   F

   T

   F

   F

   T

   F

   T

   F

   T

   T

   T

   T

   T

   F

   F

   T

   T

   F

   F

   F

   F

   F

   T

   F

   F

   F

   F

   T

   T

   F

   F

   T

   T

   F

   Look at the columns for the main connectives; biconditional for the first, conditional for the second and third. On the last four rows, all are true. Since there is at least one row of a complete truth table on which all of the sentences are true, the sentences are logically consistent.

F. Exercises: Truth table logical equivalence. Determine whether each pair of sentences is logically equivalent. Justify your answer with a complete truth table.

1. (P→P), (P↔P)
   

   P	(P	→	P)	(P	↔	P)
   T	T	T	T	T	T	T
   F	F	T	F	F	T	F

   Look at the main logical connectives, conditional and biconditional. We can see that on every row, they have the same truth value, so they are logically equivalent. Note: all tautologies are logically equivalent to one another.

2. (P↔~Q), (~P↔Q)
   

   P	Q	(P	↔	~	Q)	(~	P	↔	Q)
   T	T	T	F	F	T	F	T	F	T
   T	F	T	T	T	F	F	T	T	F
   F	T	F	T	F	T	T	F	T	T
   F	F	F	F	T	F	T	F	F	F

   Look at the main logical connectives, conditional and biconditional. We can see that on every row, they have the same truth value, so they are logically equivalent.

3. (P&~P), (~Q↔Q)
   

   P	Q	(P	&	~	P)	(~	Q	↔	Q)
   T	T	T	F	F	T	F	T	F	T
   T	F	T	F	F	T	T	F	F	F
   F	T	F	F	T	F	F	T	F	T
   F	F	F	F	T	F	T	F	F	F

   Look at the main logical connectives, conjunction and biconditional. We can see that on every row, they have the same truth value, so they are logically equivalent. Note: all contradictions are logically equivalent to one another.

4. (P↔Q), (~Q↔~P)
   

   P	Q	(P	↔	Q)	(~	Q	↔	~	P)
   T	T	T	T	T	F	T	T	F	T
   T	F	T	F	F	T	F	F	F	T
   F	T	F	F	T	F	T	F	T	F
   F	F	F	T	F	T	F	T	T	F

   Look at the main logical connectives, both biconditional. We can see that on every row, they have the same truth value, so they are logically equivalent.

5. (P↔Q) (~Q↔~P)
   

   P	Q	~	(P	↔	Q)	(~	Q	↔	~	P)
   T	T	F	T	T	T	F	T	T	F	T
   T	F	T	T	F	F	T	F	F	F	T
   F	T	T	F	F	T	F	T	F	T	F
   F	F	F	F	T	F	T	F	T	T	F

G. Exercises: Prove each of the following arguments is valid.

1. Premises: (P ∨ Q), (Q ∨ R), ~Q. Conclusion: P & R
   
2. Premises: (P ↔ Q), (Q ↔ R), Conclusion: (P ↔ R)
   
3. Premise: (P → (P & ~P),  Conclusion: ~P
   
4. Premises: P, ~Q. Conclusion: ~(P↔Q)
   
5. Premises: (~PvQ), (Pv~Q). Conclusion: (P↔Q)
   
6. Premises: (P↔Q), (R↔S) . Conclusion: ((P&R) ↔ (Q&S))
   
7. Premises: (P → ~Q), (R & P), (Q v (S & T)) Conclusion: T
   
8. Premises: (Q↔~P), (Q v ~P). Conclusion: Q
   
9. Premise: (P&Q). Conclusion: (P↔Q)
   

H. Exercises: Prove each of the following theorems. (They can be proven without any premises).

1. ~(P&~P) (principle of bivalence)
   
2. ~((P→~P)&(~P→P))
   
3. (~P→~(P&Q)).
   
4. ((P&~Q)→~(P→Q))
   
5. (P→ (Q→P))
   
6. (P&Q) →  ((P v R) & (Q v R))
   
7. (P v ~P)
   
8. (~(P→Q) ↔ (P&~Q))
   
9. (~P → (P → Q))
   
10. (P → (Q → P))
    
11. ((P→(Q→R)) → ((P→Q) → (P→R)))
    
12. ((~P→~Q) → ((~P→Q) →P))
    
13. ((P&Q) ↔~(~Pv~Q))
    
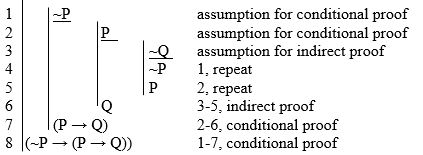
14. ((P→Q) ↔~(P&~Q))
    

I. Exercises: Answer each of the questions below and justify your answer

1. P and Q have the same truth value on every line of a complete truth table, so P ↔Q is true on every line. It is a tautology.
2. The sentence is false on some line of a complete truth table. On that line, P and Q are true and R is false. So the argument is invalid.
3. Since P is false on every line of a complete truth table, there is no line on which P and Q are true and R is false. So the argument is valid.
4. Since R is true on every line of a complete truth table, there is no line on which P and Q are true and R is false. So the argument is valid.
5. Not much. (PvQ) is a tautology if P and Q are tautologies; it is a contradiction if they are contradictions; it is contingent if they are contingent.
6. P and Q have different truth values on at least one line of a complete truth table, and (PvQ) will be true on that line. On other lines, it might be true or false. So (PvQ) is either a tautology or it is contingent; it is not a contradiction.