9. Testing for Validity – Example

Let’s determine whether the following argument is valid or invalid:

(P & Q) v R, ~(P & Q), R -> P |- ~(P & R)

We first begin by constructing one large truth table for the entire argument.  The header row also contains the commas and the ‘|-‘ symbol.

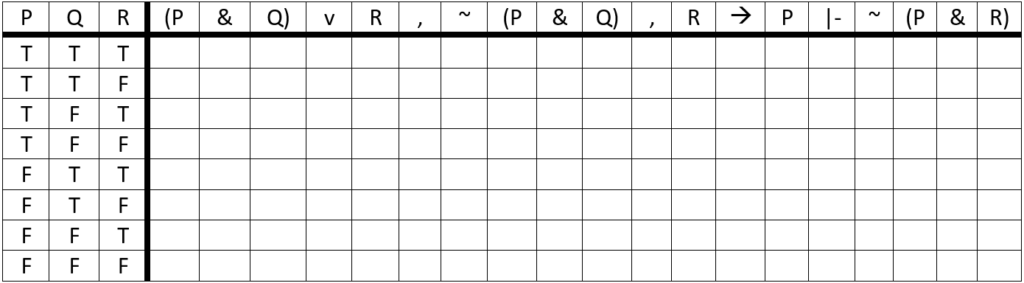
Once the table has been constructed, we simply solve for each statement found in the argument, all on the same table.  In this case, we must fill in the truth table for four statements (three premises and one conclusion.)  Be sure to highlight the governing connective for each statement, as doing so will be helpful in our later analysis.

Importantly, we treat each statement as independent from all others at this stage in our analysis.  Only when we are ready to determine whether the argument is valid or invalid do we explore the relationship between the statements.

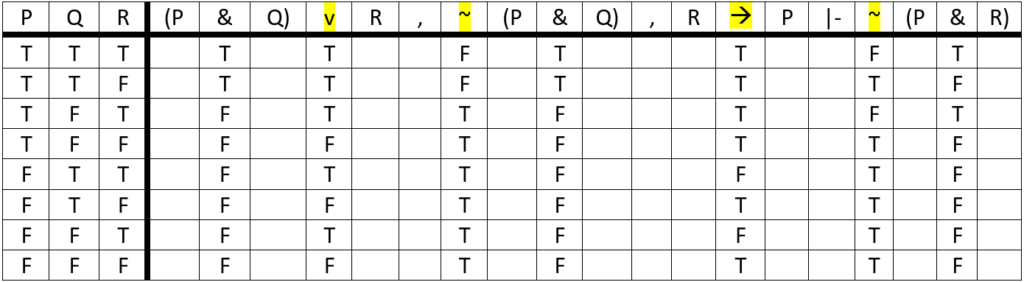
Now that our truth table has been filled in, we may determine whether this argument is valid.  To do so, use the following steps.  (Remember, at this stage of our analysis, we are only focusing on the governing connective columns in the table – the columns with the symbols highlighted in yellow.)

Step 1:  Starting at the top of the governing connective column for the conclusion, go down the column until you find an F.

Step 2:  For that F, look at the governing connectives for ALL of the premises.

Step 3:  If all the governing connectives for the premises are TRUE on that same row where the conclusion is FALSE, then you have shown that the argument is invalid.

Step 4:  If that F ‘passes the test,’ then go back to step 1, starting with the next F in the conclusion column.

Important:  If you have tested all Fs in the governing connective column of the conclusion and no evidence of invalidity appears, then the argument must be valid.

Using the above steps, we can see that the argument is invalid because the third row shows all of the premises are true (at the level of their governing connectives) and the conclusion is false.

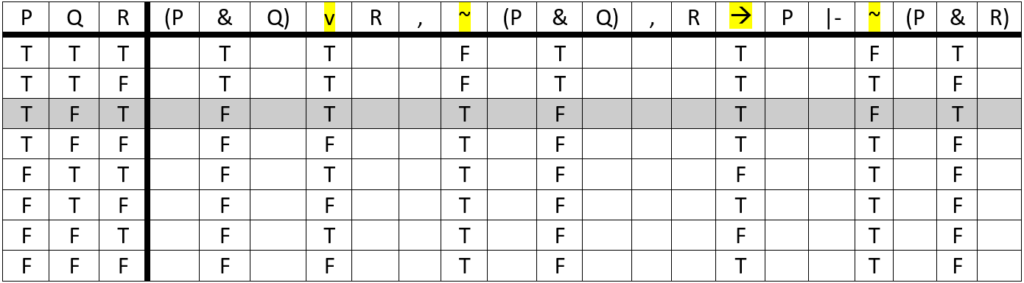
Note that for an argument to be declared invalid, there needs to be at least one row where all of the premises are true and the conclusion is false.  Even if none of the other rows would count as ‘evidence’ for the invalidity of the argument, the presence of one row proving invalidity, no matter how long or complex the truth table, is enough to declare the argument as a whole invalid.