2. “If…then…” and “It is not the case that…”

2.1 The Conditional

As we noted in chapter 1, there are sentences of a natural language, like English, that are not atomic sentences. Our examples included:

If Lincoln wins the election, then Lincoln will be President.

The Earth is not the center of the universe.

We could treat these like atomic sentences, but then we would lose a great deal of important information. For example, the first sentence tells us something about the relationship between the atomic sentences “Lincoln wins the election” and “Lincoln will be President”. And the second sentence above will, one supposes, have an interesting relationship to the sentence, “The Earth is the center of the universe”. To make these relations explicit, we will have to understand what “if…then…” and “not” mean. Thus, it would be useful if our logical language was able to express these kinds of sentences in a way that made these elements explicit. Let us start with the first one.

The sentence, “If Lincoln wins the election, then Lincoln will be President” contains two atomic sentences, “Lincoln wins the election” and “Lincoln will be President”. We could thus represent this sentence by letting

Lincoln wins the election

be represented in our logical language by

P

And by letting

Lincoln will be president

be represented by

Q

Then, the whole expression could be represented by writing

If P then Q

It will be useful, however, to replace the English phrase “if…then…” by a single symbol in our language. The most commonly used such symbol is “→”. Thus, we would write

P→Q

One last thing needs to be observed, however. We might want to combine this complex sentence with other sentences. In that case, we need a way to identify that this is a single sentence when it is combined with other sentences. There are several ways to do this, but the most familiar (although not the most elegant) is to use parentheses. Thus, we will write our expression

(P→Q)

This kind of sentence is called a conditional. It is also sometimes called a “material conditional”. The first constituent sentence (the one before the arrow, which in this example is “P”) is called the antecedent. The second sentence (the one after the arrow, which in this example is “Q”) is called the consequent.

We know how to write the conditional, but what does it mean? As before, we will take the meaning to be given by the truth conditions—that is, a description of when the sentence is either true or false. We do this with a truth table. But now, our sentence has two parts that are atomic sentences,P and Q. Note that either atomic sentence could be true or false.

 

Distributing Truth Values:

  1. To construct a truth table, we list the atomic components of a sentence Φ in alphabetical order at the top of the table, to the left of the vertical line. If Φ is (P→Q), then its components are P and Q, and they would be listed alphabetically as follows:
    P Q _
    _ _ _
    _ _ _
    _ _ _
    _ _ _

    That means, we have to consider four possible kinds of situations. We must consider when P is true and when it is false, but then we need to consider those two kinds of situations twice: once for when Q is true and once for when Q is false.

  2. To make a truth table, then, we must systematically list the combinations of truth values that the atomic portions of a sentence Φ might have. In a column under the first atomic portion of Φ, we assign the first half T (for true), and the second half F, for false. In a column under the second atomic portion of Φ, we assign the first half of the first half T (for true), and the second half of the second half F, for false. We repeat this process until a column has been entered under the last atomic portion of Φ. That column will alternate a single T (for true) with a single F (for false). Keeping with our example, the truth value assignment for (P→Q) would be as follows:
    P Q _
    T T _
    T F _
    F T _
    F F _

    There are four kinds of ways the world could be that we must consider.

    Note that, since there are two possible truth values (true and false), whenever we consider another atomic sentence, there are twice as many ways the world could be that we should consider. Thus, for n atomic sentences, our truth table must have 2n rows. In the case of a conditional formed out of two atomic sentences, like our example of (P→Q), our truth table will have 22 rows, which is 4 rows. We see this is the case above.

  3. The next step is to distribute the truth value assignment so that each atomic portion of Φ receives the same truth value assignment on the truth table. For example, whenever P appears, it receives the same truth value assignment, and whenever Q appears, Q receives the same truth value assignment. Distributing the truth value assignment for (P→Q) would be as follows:
    P Q (P → Q)
    T T T T
    T F T F
    F T F T
    F F F F

    Now, we must decide upon what the conditional means. In doing so, we want to capture as much of the meaning of the English “if…then…” as we can, while remaining absolutely precise in our language.

    Let us consider each kind of way the world could be. For the first row of the truth table, we have that P is true and Q is true. Suppose the world is such that Lincoln wins the election, and also Lincoln will be President. Then, would I have spoken truly if I said, “If Lincoln wins the election, then Lincoln will be President”? Most people agree that I would have. Similarly, suppose that Lincoln wins the election, but Lincoln will not be President. Would the sentence “If Lincoln wins the election, then Lincoln will be President” still be true? Most agree that it would be false now. So the first rows of our truth table are uncontroversial.

    P Q (P→Q)
    T T T
    T F F
    F T
    F F
  4. We write the truth value of (P→Q) under the main logical connective, →, as follows:
    P Q (P → Q)
    T T T T T
    T F T F F
    F T F T
    F F F F

Some students, however, find it hard to determine what truth values should go in the next two rows. Note now that our principle of bivalence requires us to fill in these rows. We cannot leave them blank. If we did, we would be saying that sometimes a conditional can have no truth value; that is, we would be saying that sometimes, some sentences have no truth value. But our principle of bivalence requires that—in all kinds of situations—every sentence is either true or false, never both, never neither. So, if we are going to respect the principle of bivalence, then we have to put either T or F in for each of the last two rows.

It is helpful at this point to change our example. Let us consider two different examples to illustrate how best to fill out the remainder of the truth table for the conditional.

First, suppose I say the following to you: “If you give me $50, then I will buy you a ticket to the concert tonight.” Let

You give me $50

be represented in our logic by

R

and let

I will buy you a ticket to the concert tonight.

be represented by

S

Our sentence then is

(R→S)

And its truth table—as far as we understand right now—is:

R S (R → S)
T T T T T
T F T F F
F T F T
F F F F

That is, if you give me the money and I buy you the ticket, my claim that “If you give me $50, then I will buy you a ticket to the concert tonight” is true. And, if you give me the money and I don’t buy you the ticket, I lied, and my claim is false. But now, suppose you do not give me $50, but I buy you a ticket for the concert as a gift. Was my claim false? No. I simply bought you the ticket as a gift, but, presumably would have bought it if you gave me the money, also. Similarly, if you don’t give me money, and I do not buy you a ticket, that seems perfectly consistent with my claim.

So, the best way to fill out the truth table is as follows.

R S (R → S)
T T T T T
T F T F F
F T F T T
F F F T F

Second, consider another sentence, which has the advantage that it is very clear with respect to these last two rows. Assume that a is a particular natural number, only you and I don’t know what number it is (the natural numbers are the whole positive numbers: 1, 2, 3, 4…). Consider now the following sentence.

If a is evenly divisible by 4, then a is evenly divisible by 2.

(By “evenly divisible,” I mean divisible without remainder.) The first thing to ask yourself is: is this sentence true? I hope we can all agree that it is—even though we do not know what a is. Let

a is evenly divisible by 4

be represented in our logic by

U

and let

a is evenly divisible by 2

be represented by

V

Our sentence then is

(U→V)

And its truth table—as far as we understand right now—is:

U V (U → V)
T T T T T
T F T F F
F T F T
F F F F

Now consider a case in which a is 6. This is like the third row of the truth table. It is not the case that 6 is evenly divisible by 4, but it is the case that 6 is evenly divisible by 2. And consider the case in which a is 7. This is like the fourth row of the truth table; 7 would be evenly divisible by neither 4 nor 2. But we agreed that the conditional is true—regardless of the value of a! So, the truth table must be:[3]

U V (U → V)
T T T T T
T F T F F
F T F T T
F F F T F

Following this pattern, we should also fill out our table about the election with:

P Q (P → Q)
T T T T T
T F T F F
F T F T T
F F F T F

If you are dissatisfied by this, it might be helpful to think of these last two rows as vacuous cases. A conditional tells us about what happens if the antecedent is true. But when the antecedent is false, we simply default to true.

We are now ready to offer, in a more formal way, the syntax and semantics for the conditional.

The syntax of the conditional is that, if Φ and Ψare sentences, then

(Φ→Ψ)

is a sentence.

The semantics of the conditional are given by a truth table. For any sentences Φ and Ψ:

Φ Ψ (Φ → Ψ)
T T T T T
T F T F F
F T F T T
F F F T F

Remember that this truth table is now a definition. It defines the meaning of “→”. We are agreeing to use the symbol “→” to mean this from here on out.

The elements of the propositional logic, like “→”, that we add to our language in order to form more complex sentences, are called “truth functional connectives”. I hope it is clear why: the meaning of this symbol is given in a truth function. (If you are unfamiliar or uncertain about the idea of a function, think of a function as like a machine that takes in one or more inputs, and always then gives exactly one output. For the conditional, the inputs are two truth values; and the output is one truth value. For example, put T F into the truth function called “→”, and you get out F.)

We will be learning how to make truth tables in Section 2.7.

2.2 Alternative phrasings in English for the conditional. Only if.

English includes many alternative phrasings that appear to be equivalent to the conditional. Furthermore, in English and other natural languages, the order of the conditional will sometimes be reversed. We can capture the general sense of these cases by recognizing that each of the following phrasings would be translated as (P→Q). (In these examples, we mix English and our propositional logic, in order to illustrate the variations succinctly.)

If P, then Q.

Q, if P.

On the condition that P, Q.

Q, on the condition that P.

Given that P, Q.

Q, given that P.

Provided that P, Q.

Q, provided that P.

When P, then Q.

Q, when P.

P implies Q.

Q is implied by P.

P is sufficient for Q.

Q is necessary for P.

An oddity of English is that the word “only” changes the meaning of “if”. You can see this if you consider the following two sentences.

Fifi is a cat, if Fifi is a mammal.

Fifi is a cat only if Fifi is a mammal.

Suppose we know Fifi is an organism, but, we don’t know what kind of organism Fifi is. Fifi could be a dog, a cat, a gray whale, a ladybug, a sponge. It seems clear that the first sentence is not necessarily true. If Fifi is a gray whale, for example, then it is true that Fifi is a mammal, but false that Fifi is a cat; and so, the first sentence would be false. But the second sentence looks like it must be true (given what you and I know about cats and mammals).

We should thus be careful to recognize that “only if” does not mean the same thing as “if”. (If it did, these two sentences would have the same truth value in all situations.) In fact, it seems that “only if” can best be expressed by a conditional where the “only if” appears before the consequent (remember, the consequent is the second part of the conditional—the part that the arrows points at). Thus, sentences of this form:

P only if Q.

Only if Q, P.

are best expressed by the formula

(P→Q)

2.3 Test your understanding of the conditional

People sometimes find conditionals confusing. In part, this seems to be because some people confuse them with another kind of truth-functional connective, which we will learn about later, called the “biconditional”. Also, sometimes “if…then…” is used in English in a different way (see section 17.7 if you are curious about alternative possible meanings). But from now on, we will understand the conditional as described above. To test whether you have properly grasped the conditional, consider the following puzzle.[4]

We have a set of four cards in figure 2.1. Each card has the following property: it has a shape on one side, and a letter on the other side. We shuffle and mix the cards, flipping some over while we shuffle. Then, we lay out the four cards:

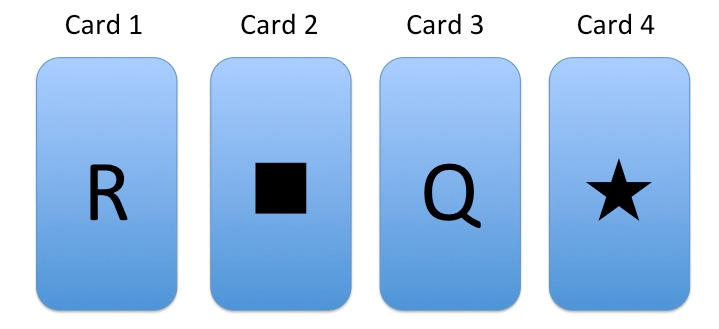
cards r square q star

 

Figure 2.1

Given our constraint that each card has a letter on one side and a shape on the other, we know that card 1 has a shape on the unseen side; card 2 has a letter on the unseen side; and so on.

Consider now the following claim:

For each of these four cards, if the card has a Q on the letter side of the card, then it has a square on the shape side of the card.

Here is our puzzle: what is the minimum number of cards that we must turn over to test whether this claim is true of all four cards; and which cards are they that we must turn over? Of course we could turn them all over, but the puzzle asks you to identify all and only the cards that will test the claim.

Stop reading now, and see if you can decide on the answer. Be warned, people generally perform poorly on this puzzle. Think about it for a while. The answer is given below in problem 1.

2.4 Alternative symbolizations for the conditional

Some logic books, and some logicians, use alternative symbolizations for the various truth-functional connectives. The meanings (that is, the truth tables) are always the same, but the symbol used may be different. For this reason, we will take the time in this text to briefly recognize alternative symbolizations.

The conditional is sometimes represented with the following symbol: “⊃”. Thus, in such a case, (P→Q) would be written

(P⊃Q)

2.5 Negation

In chapter 1, we considered as an example the sentence,

The Earth is not the center of the universe.

At first glance, such a sentence might appear to be fundamentally unlike a conditional. It does not contain two sentences, but only one. There is a “not” in the sentence, but it is not connecting two sentences. However, we can still think of this sentence as being constructed with a truth functional connective, if we are willing to accept that this sentence is equivalent to the following sentence.

It is not the case that the Earth is the center of the universe.

If this sentence is equivalent to the one above, then we can treat “It is not the case” as a truth functional connective. It is traditional to replace this cumbersome English phrase with a single symbol, “~”. Then, mixing our propositional logic with English, we would have

~The Earth is the center of the universe.

And if we let W be a sentence in our language that has the meaning The Earth is the center of the universe, we would write

~W

This connective is called negation. Its syntax is: if Φis a sentence, then

~Φ

is a sentence. We call such a sentence a “negation sentence”.

The semantics of a negation sentence is also obvious, and is given by the following truth table.

Φ ~Φ
T F
F T

To deny a true sentence is to speak a falsehood. To deny a false sentence is to say something true.

Our syntax always is recursive. This means that syntactic rules can be applied repeatedly, to the product of the rule. In other words, our syntax tells us that if P is a sentence, then ~P is a sentence. But now note that the same rule applies again: if ~P is a sentence, then ~~P is a sentence. And so on. Similarly, if P and Q are sentences, the syntax for the conditional tells us that (P→Q) is a sentence. But then so is ~(P→Q), it’s not the case that if P, then Q and so is (~(P→Q) → (P→Q)), if it’s not the case that if P, then Q, then if P, then Q, and also (~Q→P) P unless Q, or (~P→Q), Q unless P. And so on. If we have just a single atomic sentence, our recursive syntax will allow us to form infinitely many different sentences with negation and the conditional.

2.6 Alternative symbolizations for negation

Some texts may use “¬” for negation. Thus, ~P would be expressed with

¬P

2.7 How to Make a Truth Table

Truth Tables

A truth table: an explicit plotting of propositions’ truth-values.

  1. Set out the atomic sentences in alphabetic order in the leftmost column(s).
P
P Q
P Q R
P Q R S

2. Number of rows

Row = vertical dimension of truth-table

n = number of Atomic Sentences

2 to the power of n, where n = Number of Rows.

1 atomic sentences 21 = 2 Rows.

P Q

 

3 atomic sentences 23 = 8 Rows

P Q R

4 atomic sentences 24 = 16 Rows

P Q R S
  1. Number of columns.

At least one column for each distinct atomic sentence (either by itself, or as part of a dependent sentence), and at least one for each distinct dependent sentence.

e.g.

P has 1 atomic sentence, 21 = 2 Rows, and (at least) 1 column.

P

 

~P has one atomic sentence ‘P’, so it needs 21 = 2 Rows, and it has one dependent sentence, so it needs (at least) two columns. In dependent sentence columns, provide a separate sub-column for each atomic sentence that makes up the dependent sentence.

P ~ P

P → Q is a dependent sentence with two atomic sentences ‘P’ and ‘Q’. It’s truth table requires 22 = 4 Rows, and (at least) 3 columns. In the column for dependent sentences, provide a separate sub-column for each atomic sentence that makes up the dependent sentence.

P Q (P → Q)

~P→(Q→R) is a dependent sentence with three atomic sentences ‘P’ and ‘Q’ and ‘R’. It’s truth table requires 23 = 8 Rows, and (at least) 3 columns. Again, for dependent sentence columns, provide a separate sub-column for each atomic sentence that makes up the dependent sentence.

P Q R (~ P → (Q → R))

(P→Q), (Q→R), (R→S), and (P→S) are dependent sentences with four atomic sentences ‘P’, ‘Q’, ‘R’ and ‘S’. It’s truth table requires 24= 16 Rows, and (at least) 4 columns. Again, for dependent sentence columns, provide a separate sub-column for each atomic sentence that makes up the dependent sentence.

P Q R S (P → Q) (Q → R) (R → S) (P → S)
  1. Truth Value Assignment: systematic determination of the truth values of atomic sentences.

If 1 atomic sentence: use the formula 1/2n T + 1/2n F for the first column

P
T
F

Truth value of P

If 1 atomic sentence: use the formula 1/2n T + 1/2n F for the first column

P ~ P

Truth value of P

If 2 atomic sentences: use the formula 1/2n T + 1/2n F for the first column; 1/4n T + 1/4n F for the second column

P Q (P → Q)
T T
T F
F T
F F

If 3 atomic sentences: 1/2n T + 1/2n F for the first column; 1/4n T + 1/4n F for the second column, and repeat until completed; 1/8n T + 1/8n F for the third column, and repeat until completed

P Q R (~ P → (Q → R))
T T T
T T F
T F T
T F F
F T T
F T F
F F T
F F F

If 4 atomic sentences: 1/2n T + 1/2n F for the first column; 1/4n T + 1/4n F for the second column, and repeat until completed; 1/8n T + 1/8n F for the third column, and repeat until completed

P Q R S (P → Q) (Q → R) (R → S) (P → S)
T T T T
T T T F
T T F T
T T F F
T F T T
T F T F
T F F T
T F F F
F T T T
F T T F
F T F T
F T F F
F F T T
F F T F
F F F T
F F F F

And so on

  1. Distribute truth-value assignment.

Where P is T on a truth-value assignment, every instance of P on that assignment receives T; if P is F, every instance of P receives F.­­­­­­

­­

P
T
F
↑
Truth value
of P
P ~ P
T T
F F
↑
Truth value of P		 ___ ↑
Truth value of P

If 2 atomic sentences: use the formula 1/2n T + 1/2n F for the first column; 1/4n T + 1/4n F for the second column

P Q (P → Q)
T T T T
T F T F
F T F T
F F F F
↑
Truth value of P		 ↑
Truth value of P		 ↑
Truth value of P		 ___ ↑
Truth value of P

If 3 atomic sentences: use the formula 1/2n T + 1/2n F for the first column; 1/4n T + 1/4n F for the second column; 1/8n T + 1/8n F for the third column.

P Q R (~ P → (Q → R))
T T T T T T
T T F T T F
T F T T F T
F T F T F F
F T T F T T
F T F F T F
F F T F F T
F F F F F F
­ ↑
truth value
of P		 ­ ↑
truth value
of Q		 ↑­
truth value
of R		 ___ ↑­
truth value
of P		 ___ ↑­
truth value
of Q		 ___ ↑­
truth value
of R

If 4 atomic sentences: use the formula 1/2n T + 1/2n F for the first column; 1/4n T + 1/4n F for the second column; 1/8n T + 1/8n F for the third column; 1/16n T + 1/16n F for the fourth column.

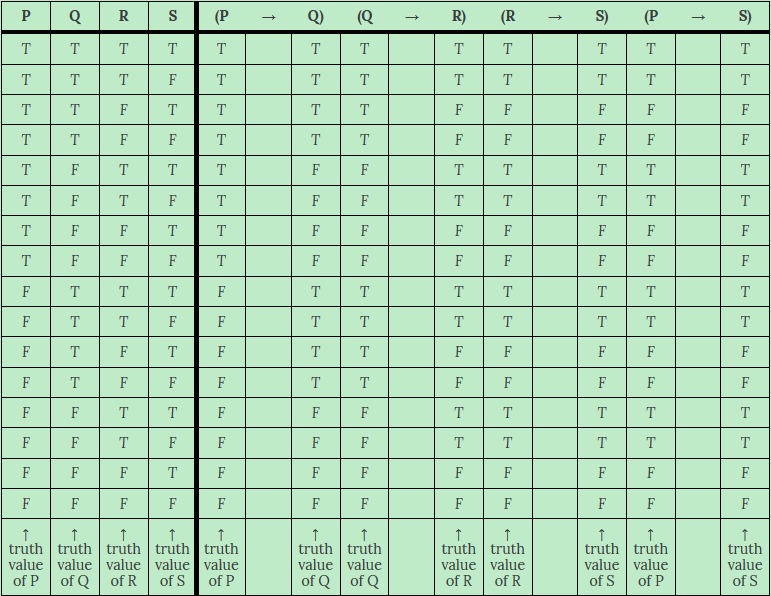
  1. Determine the truth value of target sentence(s). Use your knowledge of logical connectives to figure out the truth values of dependent sentences. For more complex sentences, there is an order: begin with inner-most parentheses (doing negations first) and move outward (still doing negations first) until you have determined the truth value of your target sentence(s).

Here, your target sentence is P itself. You have determined the truth value of P in doing your truth value assignment. P is either true or false.

P
T
F
↑
Truth value
of P

Here, your target sentence is a negation: ~P. Whenever P is true, ~P is false, and whenever P is false, ~P is true.

P ~ P
T F T
F T F
↑
Truth value
of P		 ↑
Truth value
of ~		 ↑
Truth value
of P

Here, your target sentence is a conditional: (~P→(Q→R)). ((~P→(Q→R)) is only false when the antecedent, ~P, is true and the consequent, (Q→R), is false. Otherwise, (~P→(Q→R)) is true.

P Q R (~ P → (Q → R))
T T T F T T T T T
T T F F T T T F F
T F T F T T F T T
T F F F T T F T F
F T T T F T T T T
F T F T F F T F F
F F T T F T F T T
F F F T F T F T F
___ ___ ___ ↑
Truth value
of ~P		 ___ ↑
Truth value
of (~P→(Q→R))
(Target
sentence)		 ___ ↑
Truth value
of (Q→R)		 ___
2nd 3rd 1st

Remember, do inner-most parentheses first, doing negations first, then the other connectives. Then move to outer parentheses, doing negations first then the other connectives. Continue doing this until you have determined the truth value of your target sentence(s).

In this example, you have 4 target sentences. All four are conditionals, and all four are false when their antecedent is true and their consequent is false. As these are distinct sentences, there will be four distinct truth values.

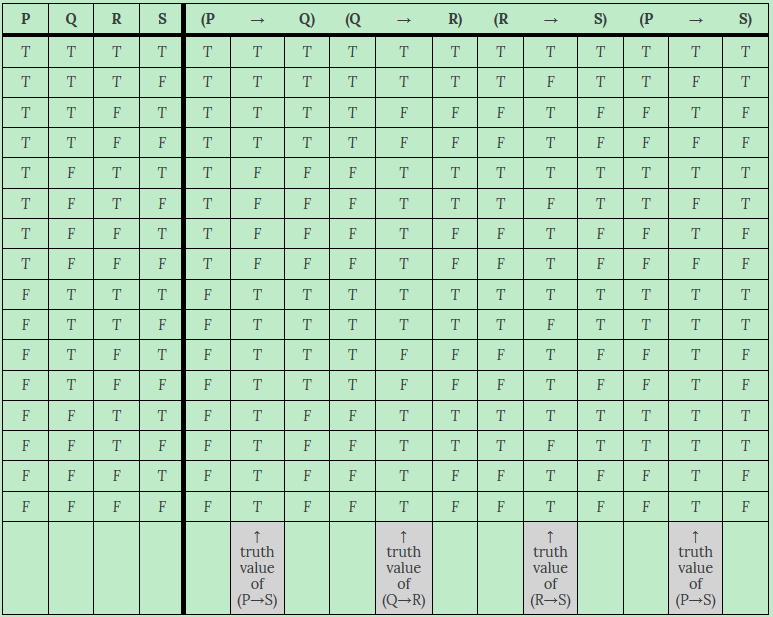
2.8 Key Concepts

If…then….” and “It is not the case that….

→: symbol for the conditional.

Conditional: a dependent sentence of the form If P, then Q. For example, if it is raining, then it is cloudy. We write “If P, then Q” as (P→Q). We call P the antecedent and Q the consequent. The sentence (P→Q) means: whenever P is true, Q must be true as well. Consider the truth table for (P→Q):

P Q (P → Q)
T T T T T
T F T F F
F T F T T
F F F T F

Look at the column for the main connective, conditional: It is false only when the antecedent is true and the consequent is false.

Antecedent: first sentence of a conditional sentence, for example P in (P→Q).

Consequent: second sentence of a conditional sentence, for example Q in (P→Q).

Vacuous truth: something that is true by default. If P is never true, then P→Q is always true. P→Q does not say anything about causality. For example, if it is never raining, then if it is raining, then it is cloudy is always true. Also, P→Q does not say anything about what happens if P is false. “If it is raining then it is cloudy” does not mean that if it is not raining, then it is not cloudy.

Asymmetrical: You cannot swap the antecedent and consequent without changing the meaning of the sentence. P→Q and Q→P mean different things. P→Q does not mean that whenever Q is true, P is true. For example, “If it is raining, then it is cloudy” does not mean that if it is cloudy, then it is raining.

P Q (P → Q) (Q → P)
T T T T T T T T
T F T F F F T T
F T F T T T F F
F F F T F F T F

Look at the truth tables for (P→Q) and (Q→P). On the second row, (P→Q) is false while (Q→P) is true, and on the third row (P→Q) is true and (Q→P) is false.

~: symbol for the negation.

Negation: a dependent sentence of the form Not P. For example, it is not raining. We write “It is not P” as ~P. The sentence ~P means: whenever P is true, ~P is false; and whenever ~P is true, P is false. Consider the truth table for ~P:

P ~ P
T F T
F T F

Look at the column for the main connective, negation : It is true when P is false, and false when P is true.

Translation key: “If…then….” and “It is not the case that….”

Translation Key: English to Propositional Logic
Logic English
P P
Not Not P
~~P P
Not Not P
(P→Q) if P, then Q
since P, Q
On the condition that P, Q
Q, on the condition that P
given that P, Q
Q, given that P
provided that P, Q
Q, provided that P
when P, then Q
Q, when P
P implies Q
Q is implied by P
P is sufficient for Q
Q is necessary for P
P only if Q
Only if Q, P
…and so on
~(P→Q) it is false that if P then Q
~P it is not the case that P
Not P
un-P
… and so on

Notes:

  1. Atomic sentences are always in the affirmative.
  2. If the meaning of a complex English sentence cannot be captured by a dependent sentence, translate it as an atomic sentence.
  3. Negations attach to only one sentence (that sentence may be atomic or dependent).
  4. Conditionals, conjunctions, disjunctions, and biconditionals each connect two and only two sentences (those sentences may be atomic or dependent).
  5. There are only two kinds of syntactically acceptable sentences in propositional logic. 1) Atomic sentences, such as P; Q; R; S, and so on, represented by capital letters, or 2) dependent sentences such as (P→Q); ~P; (P&Q); (PvQ); (P↔Q), and combinations thereof, such as ((PvQ) & ~ (P&Q)).

2.9 Exercises

Within this section, you will find two types of problems for the chapter material. Firstly there are interactive exercises that randomly test your knowledge. Secondly, there is a comprehensive list of exercise questions with all answers at the back of the text.

Interactive Exercises

A. Translating the Conditional. Determine whether each sentence should be translated as (P→Q) or as (Q→P)

B. Translating the conditional. Using the following translation key, determine whether each sentence should be translated as (R→C) or as (C→R).
Translation Key
Logic English
C It is cloudy
R It is raining

C. Conditional truth tables. Fill out the truth table for the following conditionals.

D. More complicated Conditional truth tables. Fill out the truth table for the following conditionals. If you are having difficulty, review Section 2.7 How to Make a Truth Table. Here are some truth table templates to help you determine your answers to the following questions.

E. Translating the negation. Determine whether each sentence should be translated as P, ~P or ~~P.

F.Using the following translation key, determine whether each sentence should be translated as S or ~S or ~~S A or ~A or ~~A.
Translation Key
Logic English
S It is sunny today
A She is available

G. Negation truth tables. Fill out the truth table for the following negation

H. More complicated negation truth tables. Fill out the truth table for the following negations. If you are having difficulty, review section 2.7 How to Make a Truth Table

I. Syntax. True or False? Each of the following have correct syntax (are well formed formulas).

J. Translation. Use the following translation key to translate the following sentences into a propositional logic. Don’t let it bother you if some of the sentences must be false.
Translation Key
Logic English
P Abe is able
Q Abe is honest

K. Translation. Use the following translation key to translate the following sentences into a propositional logic. Don’t let it bother you if some of the sentences must be false.
Translation Key
Logic English
C Josie is a cat
M Josie is a mammal
F Josie is a fish

L. Translation. Use the following translation key to translate the following sentences into a propositional logic. Don’t let it bother you if some of the sentences must be false
Translation Key
Logic English
A Mister Ace was murdered.
B The butler did it.
C The cook did it.
D The Duchess is lying.
E Mister Edge was murdered.
F The murder weapon was a frying pan.

M. Translation. Use the following translation key to translate the following sentences into a propositional logic. Don’t let it bother you that some of the sentences must be false.
Translation Key
Logic English
A Ava is an electrician.
H Harrison is an electrician.
F Ava is a firefighter.
I Harrison is a firefighter.
S Ava is satisfied with her career.
C Harrison is satisfied with his career.

N. Translation. Use the following translation key to translate the following sentences into a propositional logic. Don’t let it bother you if some of the sentences must be false. This problem will make use of the principle that our syntax is recursive. Translating these sentences is more challenging.
Translation Key
Logic English
P Tom will pass the exam.
T Tom studies
W Tom wakes in time.
S Steve studies
E Steve will pass the exam

O. Use the translation key in order to translate the following sentences into English. Choose the English equivalents in English sentences that seem (as much as is possible) natural
Translation Key
Logic English
R It is raining
S It is snowing

 

Full Exercise Question Sets

Click here to download a word document of blank truth tables to be filled in on the computer.

Click here to download a ready to print PDF of blank truth tables to print out and fill in by hand.

Note: both downloads above are the same tables, the PDF is just formatted to print while the word document is ready to be filled in on your computer.

Note: The following questions are full question sets that are represented within the interactive tools. Answers to all questions can be found in Answer Key appendix.

  1. Translating the Conditional. Determine whether each sentence should be translated as (P→Q) or as (Q→P)

    1. If P, then Q.
    2. Since P, Q.
    3. Q, if P.
    4. On the condition that P, Q.
    5. Q, on the condition that P.
    6. Given that P, Q.
    7. Q, given that P.
    8. Provided that P, Q.
    9. Q, provided that P.
    10. When P, then Q.
    11. Q, when P.
    12. P implies Q.
    13. Q is implied by P.
    14. P is sufficient for Q.
    15. Q is necessary for P.
    16. P only if Q.
    17. Only if Q, P.
    18. If Q, then P. (Q→P)
    19. Since Q, P.
    20. P, if Q.
    21. On the condition that Q, P.
    22. P, on the condition that Q.
    23. Given that Q, P.
    24. P, given that Q.
    25. Provided that Q, P.
    26. P, provided that Q.
    27. When Q, then P.
    28. P, when Q.
    29. Q implies P.
    30. P is implied by Q.
    31. Q is sufficient for P.
    32. P is necessary for Q.
    33. Q only if P.
    34. Only if P, Q.

  2. Translating the conditional. Using the following translation key, determine whether each sentence should be translated as (R→C) or as (C→R).

    Translation Key
    Logic English
    C It is cloudy
    R It is raining
    1. If it is raining, then it is cloudy.
    2. Since it is raining, it is cloudy.
    3. It is cloudy, if it is raining.
    4. It is raining, given that it is cloudy.
    5. Provided that it is cloudy, it is raining.
    6. It is raining, provided that it is cloudy.
    7. On the condition that it is raining, it is cloudy.
    8. It is raining, when it is cloudy.
    9. It is cloudy, on the condition that it is raining.
    10. Given that it is raining, it is cloudy.
    11. Provided that it is raining, it is cloudy.
    12. When it is cloudy, then it is raining.
    13. It is cloudy implies that it is raining.
    14. It is cloudy, provided that it is raining.
    15. It is raining is implied by it is cloudy.
    16. When it is raining, then it is cloudy.
    17. Only if it is cloudy, it is raining.
    18. If it is cloudy, then it is raining.
    19. It is cloudy is necessary for it is raining.
    20. It is raining only if it is cloudy.
    21. Since it is cloudy, it is raining.
    22. It is raining, if it is cloudy.
    23. It is raining implies that it is cloudy.
    24. It is cloudy is implied by it is raining.
    25. On the condition that it is cloudy, it is raining.
    26. It is raining, on the condition that it is cloudy.
    27. It is cloudy, when it is raining.
    28. Given that it is cloudy, it is raining.
    29. It is cloudy, given that it is raining.
    30. It is cloudy is sufficient for it is raining.
    31. It is raining is sufficient for it is cloudy.
    32. It is raining is necessary for it is cloudy.
    33. It is cloudy only if it is raining.
    34. Only if it is raining, it is cloudy.

  3. Conditional truth tables. Fill out the truth table for the following conditionals.

    1. P Q (P → Q)
    2. P Q (Q → P)

  4. More complicated Conditional truth tables. Fill out the truth table for the following conditionals. If you are having difficulty, review section 2.7 How to Make a Truth Table. Here are some truth table templates to help you determine your answers to the following questions.

    1. A B (A → B)
    2. C D (D → C)
    3. P Q ((P → Q → Q))
    4. P Q ((P → Q → P))
    5. P Q ((P → Q) → (Q → P))
    6. P Q ((Q → P) → (P → Q))

  5. Translating the negation. Determine whether each sentence should be translated as P, ~P or ~~P.

    1. Not P.
    2. It’s not not P.
    3. It is un-P.
    4. It is not un-P.
    5. P.

  6. Using the following translation key, determine whether each sentence should be translated as S or ~S or ~~S A or ~A or ~~A.

    Translation Key
    Logic English
    S It is sunny today
    A She is available
    1. It is not sunny today
    2. It is cloudy out today
    3. It is sunny out today
    4. It is not not a sunny day
    5. She is unavailable today
    6. She is available today
    7. It is not the case that she is available today
    8. She is not unavailable today

  7. Negation truth tables. Fill out the truth table for the following negations.

    1. P ~ P
    2. Q ~ Q

  8. More complicated negation truth tables. Fill out the truth table for the following negations. If you are having difficulty, review section 2.7 How to Make a Truth Table.

    1. A ~ A
    2. B ~ B
    3. P ~ ~ P
    4. P Q ~ (P → Q)
    5. P Q ~ (Q → P)
    6. P Q (~ P → ~ Q)
    7. P Q ~ (~ P → ~ Q)
    8. P Q ~ ((Q → P) → (P → Q))
    9. P Q (~ (Q → P) → (P → Q))

  9. Syntax. True or False? Each of the following have correct syntax (are well formed formulas).

    1. P
    2. (P→Q)
    3. ~(P→Q)
    4. (~P→Q)
    5. (P~→Q)
    6. (P→~Q)
    7. ~P
    8. ~~P
    9. ~P →
    10. Q
    11. (~ (P→Q) → (P~Q))
    12. ~~Q(r
    13. →~Q
    14. ~Q
    15. →~~Q
    16. (~P→~Q)
    17. ~(P~Q)
    18. ~(~P→~Q)
    19. (~ (P→Q) → (P→Q))
    20. →(~P→Q)
    21. (~ (P→Q) → ~(P→Q))
    22. (~ (P~Q) → ~(P→Q))
    23. (P→Q) ~
    24. ~(~ (P→Q) → ~(P→Q))
    25. ~→~P
    26. Q →
    27. ~(~P→~Q)
    28. (~ (P→Q) → (P→Q))
    29. (P~Q)
    30. (~P→~Q) →

  10. Translation. Use the following translation key to translate the following sentences into a propositional logic. Don’t let it bother you if some of the sentences must be false.

    Translation Key
    Logic English
    P Abe is able
    Q Abe is honest
    1. Abe is not able.
    2. Abe is not able only if Abe is not honest.
    3. Abe is able, provided that Abe is not honest.
    4. If Abe is not able then Abe is not honest.

  11. Translation. Use the following translation key to translate the following sentences into a propositional logic. Don’t let it bother you if some of the sentences must be false.

    Translation Key
    Logic English
    C Josie is a cat
    M Josie is a mammal
    F Josie is a fish
    1. Josie is a cat.
    2. Josie is a mammal.
    3. Josie is not a mammal.
    4. If Josie is not a cat, then Josie is not a mammal.
    5. Josie is a fish.
    6. Provided that Josie is a mammal, Josie is not a fish.
    7. Josie is a cat only if Josie is a mammal.
    8. Josie is a fish only if Josie is not a mammal.
    9. It’s not the case that Josie is not a mammal.
    10. Josie is not a cat, if Josie is a fish.

  12. Translation. Use the following translation key to translate the following sentences into a propositional logic. Don’t let it bother you if some of the sentences must be false

    Translation Key
    Logic English
    A Mister Ace was murdered.
    B The butler did it.
    C The cook did it.
    D The Duchess is lying.
    E Mister Edge was murdered.
    F The murder weapon was a frying pan.
    1. If Mister Ace was murdered, then the cook did it.
    2. If Mister Edge was murdered, then the cook did not do it.
    3. The cook did it only if the Duchess is lying.
    4. If the murder weapon was a frying pan, then the culprit must have been the cook.
    5. If the murder weapon was not a frying pan, then the culprit was the butler.
    6. If the murder weapon was not a frying pan, then the culprit was the cook.
    7. The Duchess is lying, unless it was Mister Edge who was murdered.
    8. If Mister Ace was murdered, he was done in with a frying pan.
    9. Since the cook did it, the butler did not.
    10. Of course the Duchess is lying.

  13. Translation. Use the following translation key to translate the following sentences into a propositional logic. Don’t let it bother you that some of the sentences must be false.

    Translation Key
    Logic English
    A Ava is an electrician.
    H Harrison is an electrician.
    F Ava is a firefighter.
    I Harrison is a firefighter.
    S Ava is satisfied with her career.
    C Harrison is satisfied with his career.
    1. If Ava is a firefighter, then she is unsatisfied with her career.
    2. It is plainly false that Ava is a firefighter, unless she is an electrician.
    3. Harrison is not unsatisfied with his career.
    4. It’s not true that Harrison is satisfied only if he is not a firefighter.
    5. Ava is satisfied with her career if Harrison is not satisfied with his.
    6. It’s not the case that Ava is satisfied with her career only if Harrison is not satisfied with his.
    7. It’s not the case that Ava is unsatisfied with her career only if Harrison is unsatisfied with his.

  14. Translation. Use the following translation key to translate the following sentences into a propositional logic. Don’t let it bother you if some of the sentences must be false. This problem will make use of the principle that our syntax is recursive. Translating these sentences is more challenging.

    Translation Key
    Logic English
    P Tom will pass the exam.
    T Tom studies
    W Tom wakes in time.
    S Steve studies
    E Steve will pass the exam
    1. It is not the case that Tom won’t pass the exam.
    2. If Tom studies, Tom will pass the exam.
    3. It is not the case that if Tom studies, then Tom will pass the exam.
    4. If Tom does not study, then Tom will not pass the exam.
    5. If Tom studies, Tom will pass the exam—provided that he wakes in time.
    6. If Tom passes the exam, then if Steve studies, Steve will pass the exam.
    7. It is not the case that if Tom passes the exam, then if Steve studies, Steve will pass the exam.
    8. If Tom does not pass the exam, then if Steve studies, Steve will pass the exam.
    9. If Tom does not pass the exam, then it is not the case that if Steve studies, Steve will pass the exam.
    10. If Tom does not pass the exam, then if Steve does not study, Steve won’t pass the exam.

  15. Use the translation key in order to translate the following sentences into English. Write out the English equivalents in English sentences that seem (as much as is possible) natural

    Translation Key
    Logic English
    R It is raining
    S It is snowing
    1. (R→S)
    2. ~~R
    3. (S→R)
    4. (~S→~R)
    5. ~(R→S)

Additional Problems

Please note that there are no answers included for these problems.

  1. The answer to our card game was: you need only turn over cards 3 and 4. This might seem confusing to many people at first. But remember the meaning of the conditional: it can only be false if the first part is true and the second part is false. The sentence we want to test is “For each of these four cards, if the card has a Q on the letter side of the card, then it has a square on the shape side of the card”. Let Q stand for “the card has a Q on the letter side of the card.” Let S stand for “the card has a square on the shape side of the card.” Then we could make a truth table to express the meaning of the claim being tested:
    Q S (Q → S)
    T T T T T
    T F T F F
    F T F T T
    F F F F F
    Look back at the cards. The first card has an R on the letter side. So, sentence Q is false. But then we are in a situation like the last two rows of the truth table, and the conditional cannot be false. We do not need to check that card. The second card has a square on it. That means S is true for that card. But then we are in a situation represented by either the first or third row of the truth table. Again, the claim that (Q→S) cannot be false in either case with respect to that card, so there is no point in checking that card. The third card shows a Q. It corresponds to a situation that is like either the first or second row of the truth table. We cannot tell then whether (Q→S) is true or false of that card, without turning the card over. Similarly, the last card shows a situation where S is false, so we are in a kind of situation represented by either the second or last row of the truth table. We must turn the card over to determine if (Q→S) is true or false of that card.
    Try this puzzle again. Consider the following claim about those same four cards: If there is a star on the shape side of the card, then there is an R on the letter side of the card. What is the minimum number of cards that you must turn over to check this claim? What cards are they?
  2. Consider the following four cards in figure 2.2. Each card has a letter on one side, and a shape on the other side.

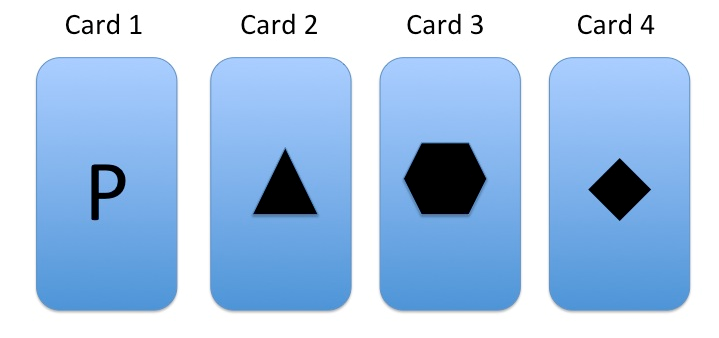
    cards p triangle hex diamond

    Figure 2.2

    For each of the following claims, in order to determine if the claim is true of all four cards, describe (1) The minimum number of cards you must turn over to check the claim, and (2) what those cards are.
    1. There is not a Q on the letter side of the card.
    2. There is not an octagon on the shape side of the card.
    3. If there is a triangle on the shape side of the card, then there is a P on the letter side of the card.
    4. There is an R on the letter side of the card only if there is a diamond on the shape side of the card.
    5. There is a hexagon on the shape side of the card, on the condition that there is a P on the letter side of the card.
    6. There is a diamond on the shape side of the card only if there is a P on the letter side of the card.
  3. Which of the following have correct syntax? Which have incorrect syntax?
    1. P→Q
    2. ~(P→Q)
    3. (~P→Q)
    4. (P~→Q)
    5. (P→~Q)
  4. Use the following translation key to translate the following sentences into a propositional logic.
    Translation Key
    Logic English
    P Abe is able.
    Q Abe is honest.
    1. If Abe is honest, Abe is able.
    2. Abe is not able.
    3. Abe is not able only if Abe is not honest.
    4. Abe is able, provided that Abe is not honest.
    5. If Abe is not able then Abe is not honest.
  5. Make up your own translation key to translate the following sentences into a propositional logic. Then, use your key to translate the sentences into the propositional logic. Your translation key should contain only atomic sentences. These should be all and only the atomic sentences needed to translate the following sentences of English. Don’t let it bother you that some of the sentences must be false.
    1. Josie is a cat.
    2. Josie is a mammal.
    3. Josie is not a mammal.
    4. If Josie is not a cat, then Josie is not a mammal.
    5. Josie is a fish.
    6. Provided that Josie is a mammal, Josie is not a fish.
    7. Josie is a cat only if Josie is a mammal.
    8. Josie is a fish only if Josie is not a mammal.
    9. It’s not the case that Josie is not a mammal.
    10. Josie is not a cat, if Josie is a fish.
  6. This problem will make use of the principle that our syntax is recursive. Translating these sentences is more challenging. Make up your own translation key to translate the following sentences into a propositional logic. Your translation key should contain only atomic sentences; these should be all and only the atomic sentences needed to translate the following sentences of English.
    1. It is not the case that Tom won’t pass the exam.
    2. If Tom studies, Tom will pass the exam.
    3. It is not the case that if Tom studies, then Tom will pass the exam.
    4. If Tom does not study, then Tom will not pass the exam.
    5. If Tom studies, Tom will pass the exam—provided that he wakes in time.
    6. If Tom passes the exam, then if Steve studies, Steve will pass the exam.
    7. It is not the case that if Tom passes the exam, then if Steve studies, Steve will pass the exam.
    8. If Tom does not pass the exam, then if Steve studies, Steve will pass the exam.
    9. If Tom does not pass the exam, then it is not the case that if Steve studies, Steve will pass the exam.
    10. If Tom does not pass the exam, then if Steve does not study, Steve won’t pass the exam.
  7. Make up your own translation key in order to translate the following sentences into English. Write out the English equivalents in English sentences that seem (as much as is possible) natural.
    1. (R→S)
    2. ~~R
    3. (S→R)
    4. (~S→~R)
    5. ~(R→S)

[3] One thing is a little funny about this second example with unknown number a. We will not be able to find a number that is evenly divisible by 4 and not evenly divisible by 2, so the world will never be like the second row of this truth table describes. Two things need to be said about this. First, this oddity arises because of mathematical facts, not facts of our propositional logic—that is, we need to know what “divisible” means, what “4” and “2” mean, and so on, in order to understand the sentence. So, when we see that the second row is not possible, we are basing that on our knowledge of mathematics, not on our knowledge of propositional logic. Second, some conditionals can be false. In defining the conditional, we need to consider all possible conditionals; so, we must define the conditional for any case where the antecedent is true and the consequent is false, even if that cannot happen for this specific example.

definition

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Elementary Formal Logic Copyright © 2020 by Jenna Woodrow and Craig DeLancey is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book