4. Proofs
4.1 A problem with semantic demonstrations of validity
Given that we can test an argument for validity, it might seem that we have a fully developed system to study arguments. However, there is a significant practical difficulty with our semantic method of checking arguments using truth tables (you may have already noted what this practical difficulty is, when you did problems 1e and 2e of chapter 3). Consider the following argument:
Alison will go to the party.
If Alison will go to the party, then Beatrice will.
If Beatrice will go to the party, then Cathy will.
If Cathy will go to the party, then Diane will.
If Diane will go to the party, then Elizabeth will.
If Elizabeth will go to the party, then Fran will.
If Fran will go to the party, then Giada will.
If Giada will go to the party, then Hilary will.
If Hillary will go to the party, then Io will.
If Io will go to the party, then Julie will.
_____
Julie will go to the party.
Most of us will agree that this argument is valid. It has a rather simple form, in which one sentence is related to the previous sentence, so that we can see the conclusion follows from the premises. Without bothering to make a translation key, we can see the argument has the following form.
P
(P →Q)
(Q→R)
(R→S)
(S→T)
(T→U)
(U→V)
(V→W)
(W→X)
(X→Y)
_____
Y
However, if we are going to check this argument, then the truth table will require 1024 rows! This follows directly from our observation that for arguments or sentences composed of n atomic sentences, the truth table will require 2n rows. This argument contains 10 atomic sentences. A truth table checking its validity must have 210 rows, and 210=1024. Furthermore, it would be trivial to extend the argument for another, say, ten steps, but then the truth table that we make would require more than a million rows!
For this reason, and for several others (which become evident later, when we consider more advanced logic), it is very valuable to develop a syntactic proof method. That is, a way to check proofs not using a truth table, but rather using rules of syntax.
Here is the idea that we will pursue. A valid argument is an argument such that, necessarily, if the premises are true, then the conclusion is true. We will start just with our premises. We will set aside the conclusion, only to remember it as a goal. Then, we will aim to find a reliable way to introduce another sentence into the argument, with the special property that, if the premises are true, then this single additional sentence to the argument must also be true. If we could find a method to do that, and if after repeated applications of this method we were able to write down our conclusion, then we would know that, necessarily, if our premises are true then the conclusion is true.
The idea is more clear when we demonstrate it. The method for introducing new sentences will be called inference rules. We introduce our first inference rules for the conditional. Remember the truth table for the conditional:
| Φ | Ψ | (Φ→Ψ) |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
Look at this for a moment. If we have a conditional like (P→Q) (looking at the truth table above, remember that this would meant that we let Φ be P and Ψ be Q), do we know whether any other sentence is true? From (P→Q) alone we do not. Even if (P→Q) is true, P could be false or Q could be false. But what if we have some additional information? Suppose we have as premises both (P→Q) and P. Then, we would know that if those premises were true, Q must be true. We have already checked this with a truth table.
| premise | premise | |||
| P | Q | (P→Q) | P | Q |
| T | T | T | T | T |
| T | F | F | T | F |
| F | T | T | F | T |
| F | F | T | F | F |
The first row of the truth table is the only row where all of the premises are true; and for it, we find that Q is true. This, of course, generalizes to any conditional. That is, we have that:
| premise | premise | |||
| Φ | Ψ | (Φ→Ψ) | Φ | Ψ |
| T | T | T | T | T |
| T | F | F | T | F |
| F | T | T | F | T |
| F | F | T | F | F |
We now capture this insight not using a truth table, but by introducing a rule. The rule we will write out like this:
(Φ→Ψ)
Φ
_____
Ψ
This is a syntactic rule. It is saying that whenever we have written down a formula in our language that has the shape of the first row (that is, whenever we have a conditional), and whenever we also have written down a formula that has the shape in the second row (that is, whenever we also have written down the antecedent of the conditional), then go ahead, whenever you like, and write down a formula like that in the third row (the consequent of the conditional). The rule talks about the shape of the formulas, not their meaning. But of course we justified the rule by looking at the meanings.
We describe this by saying that the third line is “derived” from the earlier two lines using the inference rule.
This inference rule is old. We are, therefore, stuck with its well-established, but not very enlightening, name: modus ponens. Thus, we say, for the above example, that the third line is derived from the earlier two lines using modus ponens.
4.2 Direct proof
We need one more concept: that of a proof. Specifically, we’ll start with the most fundamental kind of proof, which is called a “direct proof”. The idea of a direct proof is: we write down as numbered lines the premises of our argument. Then, after this, we can write down any line that is justified by an application of an inference rule to earlier lines in the proof. When we write down our conclusion, we are done.
Let us make a proof of the simple argument above, which has premises (P→Q) and P, and conclusion Q. We start by writing down the premises and numbering them. There is a useful bit of notation that we can introduce at this point. It is known as a “Fitch bar”, named after a logician Frederic Fitch, who developed this technique. We will write a vertical bar to the left, with a horizontal line indicating that the premises are above the line.
![Rendered by QuickLaTeX.com \[ \fitchprf{\pline[1.]{(P \lif Q)}\\ \pline[2.]{P}} { } \]](http://intrologicimport.pressbooks.tru.ca/wp-content/uploads/sites/9/2019/03/quicklatex.com-7929bb627e50374aa6a4e47bcfb11864_l3.png)
It is also helpful to identify where these steps came from. We can do that with a little explanation written out to the right.
![Rendered by QuickLaTeX.com \[ \fitchprf{\pline[1.] {(P \lif Q)} [premise]\\ \pline[2.]{P} [premise] } { } \]](http://intrologicimport.pressbooks.tru.ca/wp-content/uploads/sites/9/2019/03/quicklatex.com-1b45ba83a45f3d0ecf957ddd00581a3d_l3.png)
Now, we are allowed to write down any line that follows from an earlier line using an inference rule.
![Rendered by QuickLaTeX.com \[ \fitchprf{\pline[1.] {(P \lif Q)} [premise]\\ \pline[2.]{P} [premise] } { \pline[3.]{Q} } \]](http://intrologicimport.pressbooks.tru.ca/wp-content/uploads/sites/9/2019/03/quicklatex.com-71785cf48a0a07bc985b22fa4a819263_l3.png)
And, finally, we want a reader to understand what rule we used, so we add that into our explanation, identifying the rule and the lines used.
![Rendered by QuickLaTeX.com \[ \fitchprf{\pline[1.] {(P \lif Q)} [premise]\\ \pline[2.]{P} [premise] } { \pline[3.]{Q} [modus ponens, 1, 2] } \]](http://intrologicimport.pressbooks.tru.ca/wp-content/uploads/sites/9/2019/03/quicklatex.com-b55216bb2371272db2ee8ed6f5cd7ddd_l3.png)
That is a complete direct proof.
Notice a few things. The numbering of each line, and the explanations to the right, are bookkeeping; they are not part of our argument, but rather are used to explain our argument. However, always do them because, it is hard to understand a proof without them. Also, note that our idea is that the inference rule can be applied to any earlier line, including lines themselves derived using inference rules. It is not just premises to which we can apply an inference rule. Finally, note that we have established that this argument must be valid. From the premises, and an inference rule that preserves validity, we have arrived at the conclusion. Necessarily, the conclusion is true, if the premises are true.
The long argument that we started the chapter with can now be given a direct proof.
![Rendered by QuickLaTeX.com \[ \fitchprf{\pline[1.] {P} [premise]\\ \pline[2.]{(P \lif Q)} [premise]\\ \pline[3.]{(Q \lif R)} [premise]\\ \pline[4.]{(R \lif S)} [premise]\\ \pline[5.]{(S \lif T)} [premise]\\ \pline[6.]{(T \lif U)} [premise]\\ \pline[7.]{(V \lif W)} [premise]\\ \pline[8.]{(W \lif X)} [premise]\\ \pline[9.]{(X \lif Y)} [premise]\\ \pline[10.]{(Y \lif X)} [premise]\\ } { \pline[11.]{Q} [modus ponens, 2, 1]\\ \pline[12.]{R} [modus ponens, 3, 11]\\ \pline[13.]{S} [modus ponens, 4, 12]\\ \pline[14.]{T} [modus ponens, 5, 13]\\ \pline[15.]{U} [modus ponens, 6, 14]\\ \pline[16.]{V} [modus ponens, 7, 15]\\ \pline[17.]{W} [modus ponens, 8, 16]\\ \pline[18.]{X} [modus ponens, 9, 17]\\ \pline[19.]{Y} [modus ponens, 10, 18] } \]](http://intrologicimport.pressbooks.tru.ca/wp-content/uploads/sites/9/2019/03/quicklatex.com-d033123d5f1c22bedc5e2879e66a7395_l3.png)
From repeated applications of modus ponens, we arrived at the conclusion. If lines 1 through 10 are true, line 19 must be true. The argument is valid. And, we completed it with 19 steps, as opposed to writing out 1024 rows of a truth table.
We can see now one of the very important features of understanding the difference between syntax and semantics. Our goal is to make the syntax of our language perfectly mirror its semantics. By manipulating symbols, we manage to say something about the world. This is a strange fact, one that underlies one of the deeper possibilities of language, and also, ultimately, of computers.
4.3 Other inference rules
We can now introduce other inference rules. Looking at the truth table for the conditional again, what else do we observe? Many have noted that if the consequent of a conditional is false, and the conditional is true, then the antecedent of the conditional must be false. Written out as a semantic check on arguments, this will be:
| premise | premise | |||
| Φ | Ψ | (Φ→Ψ) | ~Ψ | ~Φ |
| T | T | T | F | F |
| T | F | F | T | F |
| F | T | T | F | T |
| F | F | T | T | T |
(Remember how we have filled out the truth table. We referred to those truth tables used to define “→” and “~”, and then for each row of this table above, we filled out the values in each column based on that definition.)
What we observe from this truth table is that when both (Φ→Ψ) and ~Ψ are true, then ~Φ is true. Namely, this can be seen in the last row of the truth table.
This rule, like the last, is old, and has a well-established name: modus tollens. We represent it schematically with
(Φ→Ψ)
~Ψ
_____
~Φ
What about negation? If we know a sentence is false, then this fact alone does not tell us about any other sentence. But what if we consider a negated negation sentence? Such a sentence has the following truth table.
| Φ | ~~Φ |
|---|---|
| T | T |
| F | F |
We can introduce a rule that takes advantage of this observation. In fact, it is traditional to introduce two rules, and lump them together under a common name. The rules’ name is double negation. Basically, the rule says we can add or take away two negations any time. Here are the two schemas for the two rules:
Φ
_____
~~Φ
and
~~Φ
_____
Φ
Finally, it is sometimes helpful to be able to repeat a line. Technically, this is an unnecessary rule, but if a proof gets long, we often find it easier to understand the proof if we write a line over again later when we find we need it again. So we introduce the rule repeat.
Φ
_____
Φ
4.4 An example
Here is an example that will make use of all three rules. Consider the following argument:
(Q→P)
(~Q→R)
~R
_____
P
We want to check this argument to see if it is valid.
To do a direct proof, we number the premises so that we can refer to them when using inference rules.
![Rendered by QuickLaTeX.com \[ \fitchprf{\pline[1.] {(Q \lif P)} [premise]\\ \pline[2.]{(\lnot Q \lif R)} [premise]\\ \pline[3.]{\lnot R} [premise]\\ } { } \]](http://intrologicimport.pressbooks.tru.ca/wp-content/uploads/sites/9/2019/03/1.png)
And, now, we apply our inference rules. Sometimes, it can be hard to see how to complete a proof. In the worst case, where you are uncertain of how to proceed, you can apply all the rules that you see are applicable and then, assess if you have gotten closer to the conclusion; and repeat this process. Here in any case is a direct proof of the sought conclusion.
![Rendered by QuickLaTeX.com \[ \fitchprf{\pline[1.] {(Q \lif P)} [premise]\\ \pline[2.]{(\lnot Q \lif R)} [premise]\\ \pline[3.]{\lnot R} [premise]\\ } { \pline[4.]{\lnot \lnot Q}[modus tollens, 2, 3]\\ \pline[5.]{Q}[double negation, 4]\\ \pline[6.]{P}[modus ponens, 1, 5]\\ } \]](http://intrologicimport.pressbooks.tru.ca/wp-content/uploads/sites/9/2019/03/2-1.png)
Developing skill at completing proofs merely requires practice. You should strive to do as many problems as you can.
4.5 How to Make a Direct Proof
Direct Proofs
A proof (or deduction): allows us to determine the validity of arguments more efficiently and more naturally than truth table techniques. A proof uses a series of discrete truth-preserving steps to move from premises to conclusion such that if the premises are true, the conclusion must be true. Each step is either a rule of inference or a rule of replacement such that whenever you have a sentence of one form you may replace it with a sentence of another form.Notation: Each line of a proof must be enumerated and justified.
- Enumerate each line of a proof.
- Justify each sentence of a proof in a justification column to the right.
- For each non-derived sentence of a proof, write “premise” or “assumption.”
- For each derived sentence of a proof, write the name of the inference rule or replacement rule used, and the sentence(s) used to infer the derived sentence, in numerical order.
- Draw a horizontal line, a “fitch bar,” between non-derived sentences (e.g. premises and assumptions) and derived sentences.
- Draw a vertical “scope” line to the left of any non-derived sentences.
Terms, Conventions and the Accessibility Rule:
Derived Sentence: a sentence obtained by applying a inference rule or a replacement rule.
Scope Line: a vertical scope line indicates the beginning and end of a proof or subproof.
Fitch Bar: a horizontal fitch bar separates non-derived sentences, assumptions and premises, from derived sentences.
Example: Proof that the following arguments are valid:
- Premises: (P→Q), P. Conclusion: Q
![Rendered by QuickLaTeX.com \[ \fitchprf{\pline[1.] {(P \lif Q)} [premise]\\ \pline[2.]{P} [premise] } { \pline[3.]{Q} [modus ponens, 1, 2] } \]](http://intrologicimport.pressbooks.tru.ca/wp-content/uploads/sites/9/2019/03/1.1.png)
- Notice that modus ponens is truth-preserving. Whenever (P→Q) and P are true, Q must be true.
P Q (P → Q) T T T T T T F T F F F T F T T F F F T F
- Notice that modus ponens is truth-preserving. Whenever (P→Q) and P are true, Q must be true.
- Premises: (P→Q), ~Q. Conclusion: ~P

- Notice that modus tollens is truth-preserving. Whenever (P→Q) and ~Q are true, ~P must be true.
P Q (P → Q) ~Q Q ~P P T T T T T F T F T T F T F F T F F T F T F T T F T T F F F F T F T F T F
- Notice that modus tollens is truth-preserving. Whenever (P→Q) and ~Q are true, ~P must be true.
- Premises: ~~P. Conclusion: P

- Notice that double negation is truth-preserving. Whenever ~~P is true, P must be true.
P ~ ~ P T T F T F F T F
- Notice that double negation is truth-preserving. Whenever ~~P is true, P must be true.
- Premises: P. Conclusion: P

- Notice that repeat is truth-preserving. Whenever P is true, P must be true.
P T F
- Notice that repeat is truth-preserving. Whenever P is true, P must be true.
4.6 Key Concepts
Proofs
Proof (also called derivation): a sequence of steps where the conclusion of an argument is validly derived from the premises through the use of truth-preserving rules of inference or replacement. Each step is either a premise, an assumption, or follows from earlier steps according to rules of inference or replacement.
Derived Sentence: a sentence obtained by applying a inference rule or a replacement rule.
Scope Line: a vertical scope line indicates the beginning and end of a proof or subproof.
Fitch Bar: a horizontal fitch bar separates non-derived sentences, assumptions and premises, from derived sentences.
Rules of Inference: truth-preserving method for introducing new sentences.
Repeat: an inference rule for any sentence: if Φ is true, then Φ must be true.
![]()
Modus Ponens: a conditional inference rule: if (Φ→Ψ) is true, and Φ is true, then Ψ must be true.
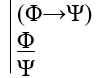
Modus Tollens: a conditional inference rule: if (Φ→Ψ) is true, and ~Ψ is true, then ~Φ must be true.
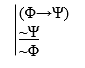
Double Negation: a rule for any sentence: if Φ is true, then ~~Φ must be true; and if ~~Φ is true, then Φ must be true.
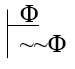 and
and 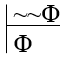
4.7 Exercises
Within this section, you will find two types of problems for the chapter material. Firstly there are interactive exercises that randomly test your knowledge. Secondly, there is a comprehensive list of exercise questions with all answers at the back of the text.
Interactive Exercises
Direct Proofs. Below are direct proofs (also called “direct derivations”) for different arguments, showing that they are valid. These proofs are incomplete. Please complete the proofs by answering the questions A and B below.
-
Justifications: Please select the appropriate justifications for each derived proposition
-
Sentences: The justifications are provided. Please enter the appropriate propositions.
Full Exercise Question Sets
Click here to download a word document of blank proofs to be filled in on the computer.
Click here to download a ready to print PDF of blank proofs to print out and fill in by hand.
Note both downloads above are the same tables, the PDF is just formatted to print while the word document is ready to be filled in on your computer.
Note: The following questions are full question sets that are represented within the interactive tools. Answers to all questions can be found in Answer Key appendix.
Direct Proofs. Below are direct proofs (also called “direct derivations”) for different arguments, showing that they are valid. These proofs are incomplete. Please complete the proofs by answering the questions A and B below.
-
Justifications: Please select the appropriate justifications for each derived proposition.
- Premises: (P→Q), P. Conclusion: Q
- Premises: (P→Q), ~Q. Conclusion: ~P
- Premises: ~~Q. Conclusion: Q
- Premises: ~Q, (~Q→S). Show: S.
- Premises: (S → ~Q), (P → S), ~~P. Show: ~Q.
- Premises: (T → P), (Q → S), (S → T), ~P. Show: ~Q.
- Premises: R, P, (P → (R → Q)). Show: Q.
- Premises: ((R → S) → Q), ~Q, (~(R → S) → V). Show: V.
- Premises: (P → (Q → R)), ~(Q → R). Show: ~P.
- Premises: (~(Q → R) →P), ~P, Q. Show: R.
- Premises: P,(P→R),(P→(R→Q)). Show: Q.
-
Sentences. The justifications are provided. Please enter the appropriate propositions.
- Premises: ~Q, (~Q→S). Show: S.
- Premises: (S→~Q), (P→S), ~~P. Show: ~Q.
- Premises: (T→P), (Q→S), (S→T), ~P. Show: ~Q.
- Premises: R, P, (P → (R → Q)). Show: Q.
- Premises: ((R→S) →Q), ~Q, (~(R→S)→V). Show: V.
- Premises: (P→(Q→R)), ~(Q→R). Show: ~P.
- Premises: (~(Q→R)→P), ~P, Q. Show: R.
- Premises: P,(P→R),(P→(R→Q)). Show: Q.
Additional Problems
Please note that there are no answers included for these problems.
-
Complete a direct derivation (also called a “direct proof”) for each of the following arguments, showing that it is valid. You will need the rules modus ponens, modus tollens, and double negation.
- Premises: ~Q, (~Q→S). Show: S.
- Premises: (S→~Q), (P → S), ~~P. Show: ~Q.
- Premises: (T→P), (Q→S), (S→T), ~P. Show: ~Q.
- Premises: R, P, (P→(R→Q)). Show: Q.
- Premises: ((R→S)→Q), ~Q, (~(R→S)→V). Show: V.
- Premises: (P→(Q→R)), ~(Q→R). Show: ~P.
- Premises: (~(Q→R)→P), ~P, Q. Show: R.
- Premises: P, (P→R), (P→(R→Q)). Show: Q.
-
In normal colloquial English, write your own valid argument with at least two premises. Your argument should just be a paragraph (not an ordered list of sentences or anything else that looks like logic). Translate it into propositional logic and use a direct proof to show it is valid.
-
In normal colloquial English, write your own valid argument with at least three premises. Your argument should just be a paragraph (not an ordered list of sentences or anything else that looks like logic). Translate it into propositional logic and use a direct proof to show it is valid.
-
Make your own key to translate into propositional logic the portions of the following argument that are in bold. Using a direct proof, prove that the resulting argument is valid.
Inspector Tarski told his assistant, Mr. Carroll, “If Wittgenstein had mud on his boots, then he was in the field. Furthermore, if Wittgenstein was in the field, then he is the prime suspect for the murder of Dodgson. Wittgenstein did have mud on his boots. We conclude, Wittgenstein is the prime suspect for the murder of Dodgson.”
A sequence of steps where the conclusion of an argument is validly derived from the premises through the use of truth-preserving rules of inference or replacement. Each step is either a premise, an assumption, or follows from earlier steps according to rules of inference or replacement (also called derivation)
Truth-preserving method for introducing new sentences.
A conditional inference rule: if (Φ→Ψ) is true, and Φ is true, then Ψ must be true
A conditional inference rule: if (Φ→Ψ) is true, and ~Ψ is true, then ~Φ must be true
A rule for any sentence: if Φ is true, then ~~Φ must be true; and if ~~Φ is true, then Φ must be true
An inference rule for any sentence: if Φ is true, then Φ must be true

