4.7 Exercises

Direct Proofs. Below are direct proofs (also called “direct derivations”) for different arguments, showing that they are valid. These proofs are incomplete. Please complete the proofs by answering the questions A and B below.

1. Justifications: Please select the appropriate justifications for each derived proposition.
   Note: Answers for part B are highlighted in each of the direct proof
   1. Premises: (P→Q), P. Conclusion: Q
      
   2. Premises: (P→Q), ~Q. Conclusion: ~P
      
   3. Premises: ~~Q. Conclusion: Q
      
   4. Premises: ~Q, (~Q→S). Show: S.
      
   5. Premises: (S → ~Q), (P → S), ~~P. Show: ~Q.
      
   6. Premises: (T → P), (Q → S), (S → T), ~P. Show: ~Q.
      
   7. Premises: R, P, (P → (R → Q)). Show: Q.
      
   8. Premises: ((R → S) → Q), ~Q, (~(R → S) → V). Show: V.
      
   9. Premises: (P → (Q → R)), ~(Q → R). Show: ~P.
      
   10. Premises: (~(Q → R) →P), ~P, Q. Show: R.
       
   11. Premises: P,(P→R),(P→(R→Q)). Show: Q.
       
2. Sentences. The justifications are provided. Please enter the appropriate propositions.
   1. Premises: P,(P→R),(P→(R→Q)). Show: S.
      
   2. Premises: (S → ~Q), (P → S), ~~P. Show: ~Q.
      
   3. Premises: (T → P), (Q → S), (S → T), ~P. Show: ~Q.
      
   4. Premises: R, P, (P → (R → Q)). Show: Q.
      
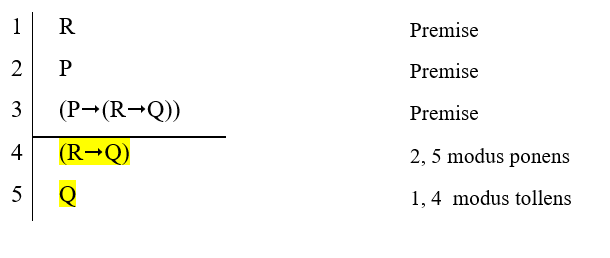
   5. Premises: ((R → S) → Q), ~Q, (~(R → S) → V). Show: V.
      
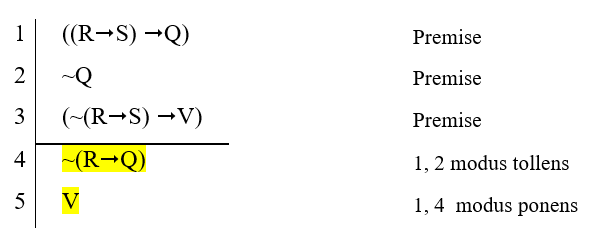
   6. Premises: (P → (Q → R)), ~(Q → R). Show: ~P.
      
   7. Premises: (~(Q → R) →P), ~P, Q. Show: R.
      
   8. Premises: P,(P→R),(P→(R→Q)). Show: Q.