Chapter 5 Answer Key

5.7 Exercises

    1. Translating conjunctions. Use the following translation key to translate the following sentences into our logical language.
      1. (C&I)
      2. ((R&Y) →H)
      3. (H→~T&C)
      4. (I&~T)
      5. ~(C&I)
    2. Conjunction truth tables. Fill out the truth table for the following conjunctions.
      P Q (P & Q)
      T T T T T
      T F T F F
      F T F F T
      F F F F F
      P Q (Q & P)
      T T T T T
      T F F F T
      F T T F F
      F F F F F
    3. Conjunction truth tables. Fill out the truth table for the following conjunctions.
      A B (A & B)
      T T T T T
      T F T F F
      F T F F T
      F F F F F
      A B (B & A)
      T T T T T
      T F F F T
      F T T F F
      F F F F F
    4. Complex truth tables. Make truth tables for the following complex sentences.
      1. (P&~Q)
        P Q (P & ~ Q)
        T T T F F T
        T F T T T F
        F T F F F T
        F F F F T F
      2. ((P&Q)&(Q&P))
        P Q ((P & Q) & (Q & P))
        T T T T T T T T T
        T F T F F F F F T
        F T F F T F T F F
        F F F F F F F F F
      3. ((P→Q) & ~Q)
        P Q ((P → Q) & ~ Q)
        T T T T T F F T
        T F T F F F T F
        F T F T T F F T
        F F F T F T T F
      4. (~P&~Q)
        P Q (~ P & ~ Q)
        T T F T F F T
        T F F T F T F
        F T T F F F T
        F F T F T T F
    5. Complex truth tables. Make truth tables for the following complex sentences. Identify which are tautologies and which are contradictions or contingent sentences.
      1. (((P→Q)& ~Q) → ~P)
        P Q (((P → Q) & ~ Q) → ~ P)
        T T T T T F F T T F T
        T F T F F F T F T F T
        F T F T T F F T T T F
        F F F T F T T F T T F

        Look at the column for the main connective, conditional: on every row, the sentence is true, so it is a tautology.

      2. ~(P&Q)
        P Q ~ (P & Q)
        T T F T T T
        T F T T F F
        F T T F F T
        F F T F F F

        Look at the column for the main connective, negation: there is at least one row where the sentence is true, and at least one row where the sentence is false, so it is contingent.

      3. ~(~P →~Q)
        P Q ~ (~ P → ~ Q)
        T T F F T T F T
        T F F F T T T F
        F T T T F F F T
        F F F T F T T F

        Look at the column for the main connective, negation: there is at least one row where the sentence is true, and at least one row where the sentence is false, so it is contingent.

      4. (P&~P)
        P (P & ~ P)
        T T F F T
        F F F T F

        Look at the column for the main connective, negation: there is at least one row where the sentence is true, and at least one row where the sentence is false, so it is contingent

    6. Truth table logical equivalence. Determine whether each pair of sentences is logically equivalent. Justify your answer with a complete truth table.
      1. P, ~P
        P ~ P
        T F T
        F T F

        Look at the main logical connectives, P itself, and negation. We can see that they do not have the same truth value on every row, so they are not logically equivalent.

      2. P, (P  →  P)
        P (P → P)
        T T T T
        F F T F

        Look at the main logical connectives, P itself, and conditional. We can see that they do not have the same truth value on every row, so they are not logically equivalent.

      3. ~(P→Q), (~P→~Q)
        P Q ~ (P → Q) (~ P → ~ Q)
        T T T T F T F T T F T
        T F F T T F F T T T F
        F T T F F T T F F F T
        F F F T T F T F T T F

        Look at the main logical connectives, negation and conditional. We can see that they do not have the same truth value on every row, so they are not logically equivalent.

      4. (P→Q), (~Q→~P)
        P Q (P → ~ Q) (~ Q → ~ P)
        T T T F F T F T T F T
        T F T T T F T F F F T
        F T F T F T F T T T F
        F F F T T F T F T T F

        Look at the main logical connectives, both conditional. We can see that they do not have the same truth value on every row, so they are not logically equivalent.

    7. Complex truth tables. Make one large truth table to show when the following sentences are true and when they are false. State which of these sentences are equivalent.
      1. ~(P&Q) (~P&~Q) ~(P→Q) (P&~Q) (~P&Q) ~(~P→~Q)
        P Q ~ (P & Q) (~ P & ~ Q) ~ (P → Q) (P & ~ Q) (~ P & Q) ~ (~ P → ~ Q)
        T T F T T T F T F F T F  T T T  T F F T F  T  F T F F T T F T
        T F T T F F F T F T F T  T F F  T T T F  F  T F F F F T T T F
        F T T F F T T F F F T F F T T  F T F T  T  F T T T T F F F T
        F F T F F F T F T T F F  F T F  F T T F  T  F F F F T F T T F

        Looking at the columns for the main connective of each sentence. We can see that on every row, ~(~P→~Q) has the same truth value as (~P&Q), so they are logically equivalent;  we can see that on every row, ~(P→Q) has the same truth value as (P&~Q), so they are logically equivalent

    8. Proofs. Complete a direct derivation (also called a “direct proof”) for each of the following arguments, showing that it is valid. You will need the rules modus ponens, modus tollens, adjunction, and simplification.
        1. Justification. Here are the answers to the proofs. Please select the appropriate justifications for each derived proposition.
          1. Premises: (P→Q)&~Q. Conclusion: ~P
          2. Premises: ((P→Q)&(R→S)), (~Q&~S). Conclusion: (~P&~R)
          3. Premises: ((R&S)→T), (Q&~T). Conclusion: ~(R&S)
          4. Premises: Premises: (P→(R→S)), (R&P). Conclusion: S
          5. Premises: Premises: (P→(R→S)), (~S&P). Conclusion: ~R
        2. Sentences. Here are the answers to the proofs. Please select the appropriate sentence for each derived proposition.
          1. Premises: (P→Q)&~Q. Conclusion: ~P
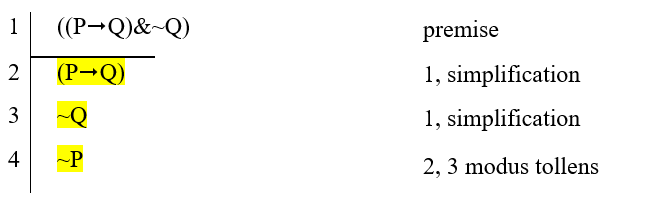
          2. Premises: ((P→Q)&(R→S)), (~Q&~S). Conclusion: (~P&~R)
          3. Premises: ((R&S)→T), (Q&~T). Conclusion: ~(R&S)
          4. Premises: Premises: (P→(R→S)), (R&P). Conclusion: S
          5. Premises: Premises: (P→(R→S)), (~S&P). Conclusion: ~R

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Elementary Formal Logic Copyright © 2020 by Jenna Woodrow and Craig DeLancey is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book