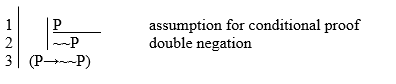Chapter 6 Answer Key
6.6 Exercises
A. Exercises: Conditional Proofs. Prove the following arguments are valid. These will require conditional proofs.
- Premises: P, Q. Conclusion: (P→Q).

- Premises: (P→Q), (Q→R). Conclusion: (P→R)

- Premise: (P→Q), (S→R). Conclusion: ((~Q & ~R) → (~P & ~S).

- Premise: (P→Q). Conclusion: ((P & R) →Q)

- Premise: ((R&Q) → S), (~P→(R&Q)). Conclusion: (~S→P)

- Premise: (P→~Q). Conclusion: (Q→~P)

- Premises: (P→Q), (P→R). Conclusion: (P→(Q&R))

- Premises: (P→(Q→R)), Q. Conclusion: (P→R)

B. Exercises: Theorems. Prove the following theorems.
- (P→P)
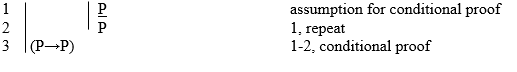
- ((P→Q)→((R→P)→(R→Q)))

- ((P→(Q→R))→((P→Q)→(P→R))

- ((~P→Q) → (~Q→P))

- (((P→Q) & (P→R)) → (P→(Q&R)))

C. Exercises: Tautologies and Theorems. Make a truth table for each of the following complex sentences. Identify which are tautologies. Prove the tautologies.
- ((P→Q)→Q)
P Q ((P → Q) → Q) T T T T T T T T F T F F T F F T F T T T T F F F T F F F - (P→(P→Q))
P Q ((P → Q) → P) T T T T T T T T F T F F T T F T F T T F F F F F T F F F - (P→(Q→P))
P Q ((P → (Q → P) T T T T T T T T F T T F T T F T F T T T F F F F T F F F Look at the main connective, conditional: on every row it is true, so it is a tautology. ((P → (Q → P) is, therefore, also a theorem, and provable from no premises.

- (P→~P)
P (P → ~ P) T T F F T F F T T F - (P→~~P)
P (P → ~ ~ P) T T T T F T F F T F T F Look at the main connective, conditional: on every row it is true, so it is a tautology. (P → ~~P) is, therefore, also a theorem, and provable from no premises.