7. Filling in a Truth Table – An Alternative Approach

Nested Governing Connectives:

Another way of conceptualizing how to fill in truth tables focuses on identifying ‘nested’ governing connectives.  The basic approach is to parse through a problem to get a point where logical operators are able to operate on ‘simple’ columns.

Logical operators in our system may be unary or binary.  The negation (~) is a unary operator, meaning that the operator is able to perform its operation only when the input is truth values from one column.  The remaining operators are binary, meaning that they are able to perform their operations only when the truth values from two columns are used as inputs.

Consider the following two basic examples:

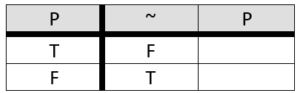
~P

As a unary operator, the negation requires one set of inputs to perform its operation.  From the perspective of the negation, the logical expression it wants to work on (P) is already a simple column.

P & Q

As a binary operator, the conjunction requires two sets of inputs to perform its operation.  From the perspective of the conjunction, the inputs of (P) and (Q) are already simplified.

Truth tables become more difficult when more operators and atomic sentences are present in the logical expression being evaluated.  In order to determine the proper order of operations to solve for the statement as a whole, we need to be thinking about the governing connective.

Recall that the governing connective of an expression in propositional logic is determined by the following two rules:

The governing connective is…

• (1) The operator most outside of all the brackets.
• (2) If there are multiple operators most outside of all the brackets, then the governing connective is whatever operator that is not the negation sign (~).

Consider the following example:

(P & Q) v Q

What is the governing connective?  In other words, what is the operator that is filled in last on our truth table?

In this case, the governing connective is the disjunction (v), as it is the operator most outside of all the brackets.

As a binary operator, the disjunction must compare two sets of inputs in order to perform its operation.  The disjunction is composed of two parts:  (P & Q) as the left disjunct, and Q as the right disjunct.  Q is already ‘reduced down’ to a simple column of truth values, as we know the values of Q from our starting resources.  (P & Q), on the other hand, is not yet ‘reduced down’ to a simple column of truth values.  Since the disjunction operation can only take place when both inputs are clearly known, we must turn our attention to (P & Q).

For the purposes of this strategy, we temporarily ignore the rest of the logic problem and focus solely on (P & Q).  Let us treat (P & Q) as if it were a separate problem.

We ask the same question:  what is the governing connective for this portion of the problem, ignoring the rest of it?  The conjunction (&).  As a binary operator, the conjunction must compare two sets of inputs in order to perform its operation.  From the perspective of the conjunction, the two inputs are P and Q.  Are we able to perform that operation?  The answer is only if both inputs are already simple columns where the truth values are already known.  In this case, both P and Q are known, so we are able to perform the operation.

Now, we return to the problem as a whole.  We want to know whether, from the perspective of the disjunction, the operation can be performed.  We already know the values for the right disjunct Q.  We now know the values for the left disjunct, P & Q – we just did work to ‘simplify’ P & Q down to one set of values.  So, we are now able to perform the disjunction operation.

This strategy focuses on identifying governing connectives, and then determining if the unary or binary operation can be performed with ‘simple’ inputs.  If the answer is no, then we move further into the problem.  We temporarily treat the complicated portion as a separate problem, determine its governing connective, and ask whether the operation can be performed.  If the answer is no, we keep repeating these steps until we find and isolate a portion of the overall problem that can be completed using the starting resources as the simple inputs for the operation.

Here is another problem:

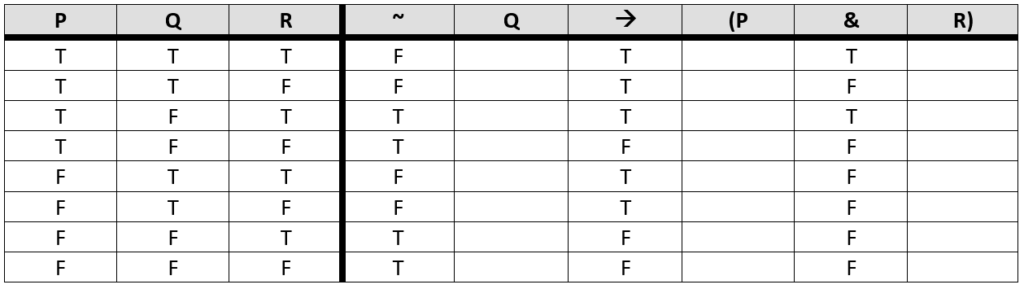
~Q -> (P & R)

The first thing we should note is that this problem involves three distinct atomic sentences.  The starting resources of our truth table must account for all possible combinations of truth values for P, Q, and R.

First, we must determine the governing connective of the problem.  We look to find the governing connective that is most outside of all the brackets.  In this case, there are two operators most outside of all the brackets:  the negation (~) and the conditional (->).  Since there are multiple operators most outside of all the brackets, we appeal to the rule where the governing connective is whatever operator that is not the negation sign(s).  So, the governing connective is the conditional.

The conditional is a binary operator:  it uses two simple columns of truth values as inputs to produce its output.  From the perspective of the conditional, the left portion of the conditional (the antecedent) is ~Q, and the right portion of the conditional (the consequent) is (P & R).  Neither portion of the conditional is a simple column of truth values.  So, according to this method, we treat this complicated portion as a problem on its own and repeat the same line of thinking.  Let’s focus on ~Q, temporarily ignoring the rest of the problem.

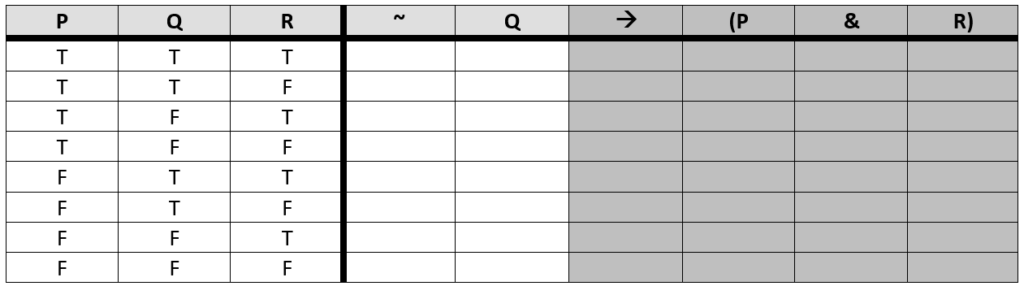
We ask ourselves what the governing connective for this ‘mini’ problem is:  the negation.  The negation is a unary operator, which means it wants one simple column of truth values as the input in order to perform its operation.  We already know what Q is, given that the column of truth values for Q is in our starting resources.  So, we are able to perform the operation.

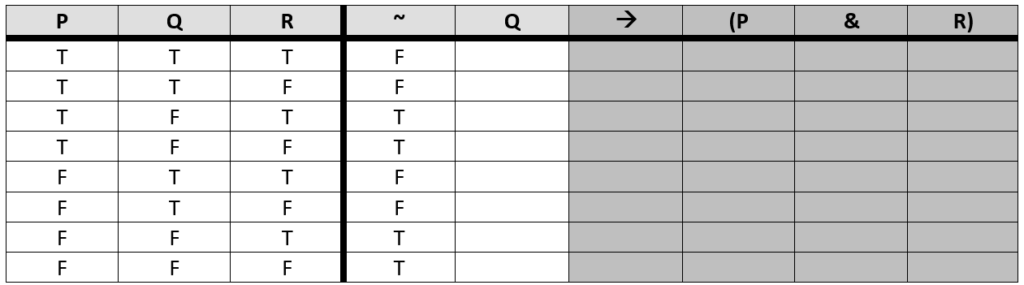
We have completed the ‘mini’ problem of ~Q.  From the perspective of the conditional, we have reduced the left portion down to one simple column of truth values – the negation column.  Next, we move onto the ‘mini’ problem of (P & R), ignoring the rest of the problem (including the work we just did).

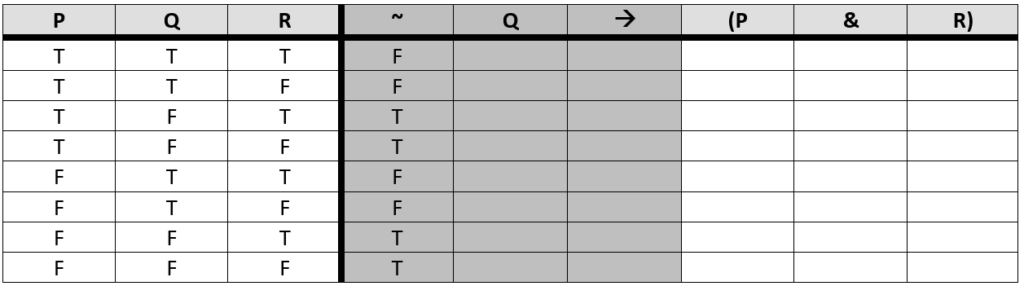
We ask ourselves what the governing connective for this new ‘mini’ problem is:  the conjunction (&).  The conjunction is a binary operator, which means it wants two simple columns of truth values as inputs in order to perform its operation.  We already know what P and R are, given that the column of truth values for P and R are in our starting resources.  So, we perform the operation.

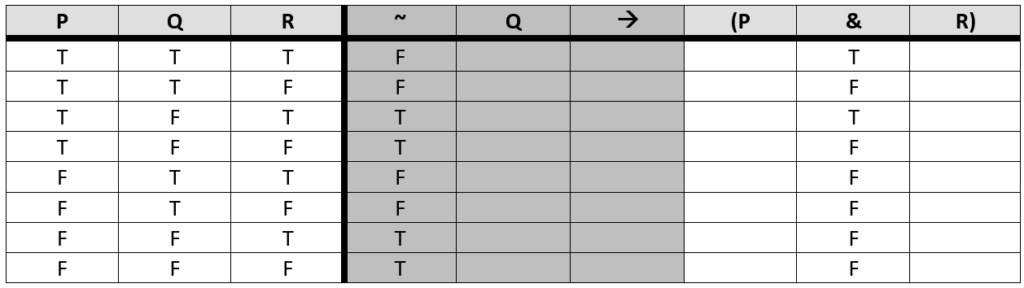
Now, from the perspective of the conditional, the governing connective of the problem overall, both the left and right portions of the problem have been reduced to simple columns of truth values; these columns can now be used as inputs for the conditional operation.