3. Logical Operators

While atomic sentences represent ideas or statements within an expression of language that can be either true or false, logical operators represent the relationship or connection between the atomic sentences.  Put differently, logical operators mark out the various ways that ideas are connected in the context of an argument.  If atomic sentences are the ‘raw material’ of an argument, then logical operators provide structure to the raw material, allowing something like an argument to take shape.

For our logical system, there are five operators:

AND
OR
IF…THEN…
IF AND ONLY IF
NOT

We are familiar with these operators as expressions in language, but we are now going to assert that these five expressions are not part of any atomic sentence, any statement.  Instead, these five expressions mark out the five ways ideas can be organized within the context of an argument and dictate the ‘truth properties’ of a given expression or argument.  We will be exploring these operators in more detail later in the text, but the following is an introductory definition for each operator.

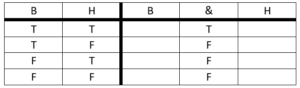
AND (Conjunction)

Represented with:  &

Example:  The keys are in the bedroom, and I am hungry.

Let’s represent the statements using atomic sentences.

B and H

Now, we are going to use the ‘&’ to represent the ‘and.’

B & H

Definition:  Produces a TRUE only when both inputs are TRUE; otherwise, produces a FALSE.

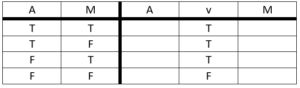
OR (Disjunction)

Represented with:  v

Example:  This thing is an apple, or I am mistaken.

Let’s represent the statements using atomic sentences.

A or M

Now, we are going to use the ‘v’ to represent the ‘or.’

A v M

Definition:  Produces a FALSE only when both inputs are FALSE; otherwise, produces a TRUE.

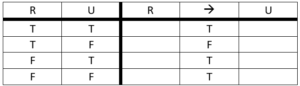
IF…THEN… (Conditional)

Represented with:  ->

Example:  If it is raining out, then I need my umbella.

Let’s represent the statements using atomic sentences.

If R, then U

Now, we are going to use the ‘à’ to represent the ‘if…then….’

R -> U

Definition:  Produces a FALSE only when the left input (antecedent) is TRUE and the right input (consequent) is FALSE; otherwise, produces a TRUE.

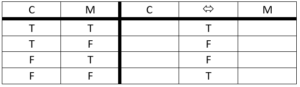
IF AND ONLY IF (Biconditional)

Represented with:  <->

Example:  It is cloudy if and only if there is a lot of moisture in the air.

Let’s represent the statements using atomic sentences.

C if and only if M

Now, we are going to use the ‘ó’ to represent the ‘if and only if.’

C <-> M

Definition:  Produces a TRUE only when both inputs are the same truth value; otherwise, produces a FALSE.

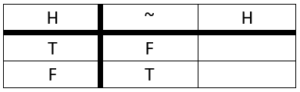
NOT (Negation)

Represented with:  ~

Example:  It is not hot outside.

Let’s represent the statements using atomic sentences.

Not H

(This representation is a bit awkward, but the key part here is that the ‘not’ is not a part of the statement itself.)

Now, we are going to use the ‘~’ to represent the ‘not.’

~H

Definition:  Produces the opposite truth value of the input.